Oppaat: Ohjelmoijan matematiikka: Osa 4 - Tiedosta dataan
Kirjoittaja: Antti Laaksonen (2007).
Tämän oppaan aiheita yhdistää tavoite muuttaa tietoa tietokoneelle sopivaan muotoon. Tietokone ymmärtää tunnetusti vain ykkösiä ja nollia, minkä vuoksi tieto täytyy tavalla tai toisella saattaa niistä muodostuvaksi. Lisäksi pyritään vielä siihen, että muutettu tieto veisi mahdollisimman vähän tilaa tietokoneen muistissa. Oppaan loppuosassa tutkitaan, kuinka osajoukkoja on mahdollista käsitellä tehokkaasti bittioperaatioiden avulla.
Bittiyhdistelmät
Tietokoneessa pienin tiedon yksikkö on bitti, joka on joko 0 tai 1. Yhdellä bitillä voidaan esittää tieto, jolla on kaksi mahdollista arvoa. Esimerkkejä ovat parit "kyllä" ja "ei", "päälle" ja "pois" sekä "musta" ja "valkoinen". Kun bittejä pannaan peräkkäin, voidaan tallentaa yhtä monta tietoa kuin on eri bittiyhdistelmiä.
Seuraavassa kuvassa näkyvät kaikki kolmen bitin yhdistelmät:
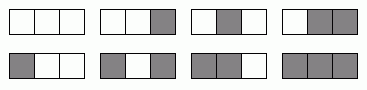
Näin tiedetään, että kolmella bitillä on mahdollista esittää kahdeksan eri tietoa. Samaan tulokseen päästään, kun huomataan, että ensimmäisen bitin arvon voi valita kahdella tavalla, samoin toisen ja kolmannenkin. Eri yhdistelmiä on siis 2 * 2 * 2 = 8. Yleisemmin n bitillä voidaan muodostaa 2n eri yhdistelmää.
Jos todellinen arvojen määrä ei ole kakkosen potenssi, osa bittiyhdistelmistä jää käyttämättä. Esimerkiksi jos täytyy tallentaa yksi numeromerkki (0 - 9), joudutaan ottamaan käyttöön neljä bittiä. Tällöin kuudestatoista mahdollisesta arvosta tarvitaan vain kymmentä. Kuitenkin kolme bittiä riittäisi vain kahdeksalle eri arvolle.
Esimerkki: Ohjelmointikielessä on muuttuja, jonka tilanvaraus on 16 bittiä. Kuinka monta eri arvoa sillä voidaan esittää?
Vastaus: Eri arvoja on 216 eli 65536. Jos muuttujaan tallennetaan kokonaisluku, muuttujan arvoalue voisi olla -32768 – 32767. Jos muuttujaan tallennetaan liukuluku, monia lukuja ei voida esittää tarkasti, koska mahdollisuuksia on kaikkiaan vain 65536, mutta reaalilukuja on äärettömästi. Tästä johtuvat pyöristysvirheet tietokoneen laskennassa.
Esimerkki: Huijari väittää kehittäneensä pakkausmenetelmän, jolla mikä tahansa 100 bitin jono voidaan tiivistää 99 bittiin. Pakkaus ei siis ole kovinkaan tehokas, mutta varmatoiminen. Osoita, että kyseessä on huijaus.
Vastaus: Kun jostain ilmestyy pakattu 99 bitin jono, se pitää pystyä palauttamaan alkuperäiseksi 100 bitin jonoksi. Kuitenkin 100 bitin jonoja on 2100 erilaista, mutta 99 bitin jonoja on vain 299 erilaista. Tämän vuoksi kaikkia 100 bitin jonoja ei pysty tiivistämään niin, että palautus onnistuisi luotettavasti. Itse asiassa jos huijarin menetelmä toimisi, mikä tahansa bittijono voitaisiin lyhentää bitti kerrallaan noin sataan bittiin.
Kokonaisluvut
Kun n bitillä voidaan esittää 2n eri tietoa, niiden avulla voidaan tallentaa vaikkapa kokonaisluku, jonka arvoalue on nollasta lukuun 2n - 1. Esimerkiksi jos käytössä on kolme bittiä, tähän tilaan voidaan tallentaa kokonaisluku väliltä 0 – 7. Eri lukuja vastaavat bittiyhdistelmät voitaisiin valita seuraavasti:
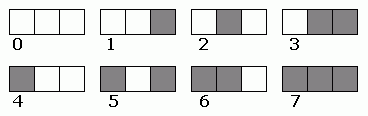
Luonnollinen tapa ilmoittaa luku bitteinä on muuttaa se binääriluvuksi. Tämä tarkoittaa, että luvut muodostetaan muuten samoin kuin kymmenjärjestelmässä, mutta ainoat numerot ovat 0 ja 1. Ensimmäiset binääriluvut ovat siis 0, 1, 10, 11, 100, 101, 110 ja 111. Jos nämä luvut muutetaan kolminumeroisiksi etunollien avulla, tulos vastaa kuvaa.
Kokonaisluvun voi muuttaa binääriluvuksi jakamalla sitä kakkosella, kunnes tulos on nolla, ja lukemalla jakojäännökset käänteisessä järjestyksessä. Esimerkiksi seuraavasta huomataan, että luku 23 on binäärilukuna 10111.
- 23 / 2 = 11, jää 1
- 11 / 2 = 5, jää 1
- 5 / 2 = 2, jää 1
- 2 / 2 = 1, jää 0
- 1 / 2 = 0, jää 1
Jokainen binääriluvun bitti vastaa yhtä kakkosen potenssia. Jos bitti on yksi, tämä kakkosen potenssi lasketaan mukaan tulokseen. Esimerkiksi binääriluvussa 10111 ykkösbittejä ovat oikealta laskien bitit 0, 1, 2 ja 4. Niinpä 20 + 21 + 22 + 24 = 1 + 2 + 4 + 16 = 23.
Ohjelmoinnissa bittejä ei tarvitse yleensä laskea itse, vaan kun lukumuuttujaan sijoitetaan arvo, se muuttuu joka tapauksessa biteiksi tietokoneen sisällä. Luvun arvoon ei tietenkään vaikuta, ilmoitetaanko se tutussa kymmenjärjestelmässä vai tietokoneen binäärijärjestelmässä.
Lukuyhdistelmät
Bittiyhdistelmissä huomattiin, että jos jokaisella yhdistelmään kuuluvalla tiedolla on kaksi arvoa, yhdistelmien kokonaismäärä saatiin kakkosten kertolaskuna. Nyt tutkitaan tilannetta, jossa kullakin tiedolla voi olla enemmän mahdollisia arvoja.
Esimerkki: Parkkitalossa on viisi kerrosta, kussakin kerroksessa kahdeksan riviä ja kullakin rivillä kymmenen paikkaa. Kuinka monta autoa parkkitaloon mahtuu?
Vastaus: Paikkoja ovat mm. "kerros 2, rivi 7, paikka 1" ja "kerros 3, rivi 3, paikka 6". Kerros voidaan valita viidellä tavalla, rivi kahdeksalla tavalla ja paikka kymmenellä tavalla, joten paikkoja on yhteensä 5 * 8 * 10 = 400.
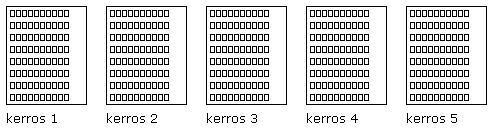
Eri yhdistelmien kokonaismäärä saadaan siis kertomalla keskenään yhdistelmään kuuluvien tietojen eri arvojen määrät. Nyt halutaan, että jokaiseen parkkitalon paikkaan voidaan viitata myös yhdellä kokonaisluvulla. Miten numerointi kannattaa valita, jotta numerosta on helppo selvittää paikan sijainti ja päinvastoin?
Esimerkki: Parkkitalon paikat halutaan numeroida kokonaisluvuilla nollasta alkaen. Miten tietyn paikan numero saadaan selville, kun tiedetään kerros, rivi ja paikka?
Vastaus: Numero voidaan laskea kaavalla (k * 8 + r) * 10 + p, kun k tarkoittaa kerrosta, r riviä ja p paikkaa. Esimerkiksi paikan "kerros 2, rivi 7, paikka 1" numero on (1 * 8 + 6) * 10 + 0 = 140. Kaavassa kerrosten, rivien ja paikkojen laskeminen aloitetaan siis nollasta.
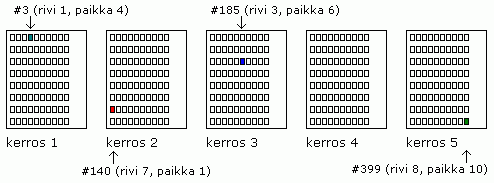
Nollasta laskien kerros, rivi ja paikka sijoittuvat aina vastaavasti lukualueille 0 – 4, 0 – 7 ja 0 – 9. Kun tutkitaan parkkitalon kaikkia rivejä, jokaiselle riville voidaan laskea oma numero kertomalla kerroksen numero 8:lla ja lisäämällä tulokseen rivin numero. Kun rivin numero on korkeimmillaan 7, näin estetään kipuaminen ylempään kerrokseen, jolloin kahdelle riville voisi tulla sama numero.
Kun kaikkien rivien numerot ovat tiedossa, samaa menetelmää voidaan soveltaa edelleen yksittäisiin paikkoihin. Kaavan muodostusta voi ajatella niin, että kertoimet valitaan juuri riittävän suuriksi, jotta eri yhdistelmät eivät sotkeudu keskenään, mutta samalla numerointi on niin tiivis, että siihen riittävät ensimmäiset kokonaisluvut nollasta alkaen.
Vastaavalla tavalla voidaan aina muodostaa kaava, jolla yhdistelmän osista saadaan kokonaisluku väliltä 0 – (n - 1), kun n on yhdistelmien kokonaismäärä. Seuraavassa pienet kirjaimet tarkoittavat yhdistelmän osien arvoja ja suuret kirjaimet tarkoittavat yhdistelmän osien eri arvojen määriä.
(((a * B + b) * C + c) * D + d) * E + e ...
Kaavaa jatketaan niin pitkälle, kuin yhdistelmän osia riittää. Aiemmassa esimerkissä kertoimet A, B ja C saavat arvot 5, 8 ja 10, ja laskettaessa paikan "kerros 2, rivi 7, paikka 1" numeroa a, b ja c saavat arvot 1, 6 ja 0. Olennaista on, että a, b ja c ovat pienimmillään 0 ja suurimmillaan A - 1, B - 1 ja C - 1. Ensimmäisen osan kerrointa A ei tarvita kaavassa lainkaan.
Esimerkki: Parkkitalon paikan numeron tiedetään olevan 185. Missä paikka sijaitsee?
Vastaus: Tämä saadaan selville käänteisesti jakolaskuilla.
- 185 / 10 = 18, jää 5
- 18 / 8 = 2, jää 2
- 2 / 5 = 0, jää 2
Kun muistetaan, että kaavassa numerointi alkoi nollasta, päästään takaisin lähtötilanteeseen "kerros 3, rivi 3, paikka 6". Viimeinen jakolasku ei ole oikeastaan tarpeellinen, niin kuin kaavassakaan ei esiintynyt tätä kerrointa, koska viimeisen jakolaskun jakojäännös on toiseksi viimeisen laskun osamäärä.
Tämä kaava toimii toki silloinkin, kun yhdistelmä muodostuu biteistä. Silloin vain aina kerrotaan ja jaetaan kakkosella. Jos osien eri arvojen määrät vaihtelevat, tilannetta voi ajatella erikoisena lukujärjestelmänä, jossa luvun eri kohdissa on käytössä eri määrä numeroita.
Esimerkki: RGB-väri muodostuu kolmesta osasta (punainen, vihreä, sininen), joista jokainen on kokonaisluku välillä 0 – 255. Millä kaavalla osista saadaan yksi kokonaisluku? Miten väri (120, 85, 200) voidaan esittää kokonaislukuna?
Vastaus: Jokaisella osavärillä on 256 arvoa, joten kaava on (R * 256 + G) * 256 + B. Väri (120, 85, 200) on kokonaislukuna (120 * 256 + 85) * 256 + 200 = 7886280.
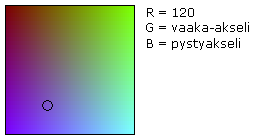
Esimerkki: RGB-värin kokonaislukuesitys on 1684515. Mistä osista väri muodostuu?
Vastaus: Selvitetään osat jakolaskulla: 1684515 / 256 = 6580, jää 35. 6580 / 256 = 25, jää 180. Värin osat ovat (25, 180, 35). Tässä vältettiin viimeinen jakolasku katsomalla punaisuuden arvo suoraan edellisen jakolaskun osamäärästä.
Esimerkki: Muuta sekunneiksi 5 päivää, 3 tuntia, 20 minuuttia ja 8 sekuntia.
Vastaus: Vuorokauteen kuuluu 24 tuntia, tuntiin kuuluu 60 minuuttia ja minuuttiin kuuluu 60 sekuntia. Kaava on ((d * 24 + h) * 60 + m) * 60 + s, joten tulos on ((5 * 24 + 3) * 60 + 20) * 60 + 8 = 444008. Tässä päivien määrää ei ole rajoitettu, mutta kaavan ensimmäisessä muuttujassa tämä ei haittaa. Tällainen lasku on muuten esiintynyt joskus aiemminkin.
Osajoukon esitys
Ohjelmoinnissa tulee usein tilanteita, joissa täytyy pitää kirjaa, mitkä tiettyyn joukkoon kuuluvista alkioista ovat valittuna. Toisin sanoen ohjelman täytyy pitää muistissa joukon osajoukkoa. Esimerkiksi viikonpäivien joukon {ma, ti, ke, to, pe, la, su} osajoukkoihin kuuluvat {ma, ke, pe} ja {la, su} sekä tyhjä joukko. Joukoissa alkioiden järjestyksellä ei ole merkitystä.
Osajoukon voi tallentaa mainiosti tavalliseen taulukkoon, jolloin ilmoitetaan erikseen, mitkä alkiot kuuluvat osajoukkoon. Mutta jos alkioiden yhteismäärä on pieni, ovelampi ratkaisu on käyttää bittitaulukkoa. Siinä jokaista valittavaa alkiota vastaa yksi bitti, joka paljastaa, onko alkio mukana osajoukossa.
Seuraavassa näkyy osajoukon {ma, ke, pe} esitys tavallisesti ja bittitaulukkona. Viikonpäiviä on seitsemän, joten jokainen niistä voidaan ilmoittaa kolmella bitillä. Tavallisessa taulukossa ilmoitetaan vain osajoukkoon kuuluvat viikonpäivät. Bittitaulukossa taas näkyvät kaikki viikonpäivät, ja valittuna olevien viikonpäivien bitit ovat ykkösiä.
Tavallinen taulukko: 000, 010, 100
Bittitaulukko: 1, 0, 1, 0, 1, 0, 0
Seitsemällä bitillä voidaan ilmaista 27 = 128 eri arvoa. Ei ole sattumaa, että seitsemän alkion joukosta voidaan myös muodostaa 128 eri osajoukkoa. Jokainen alkio joko kuuluu tai ei kuulu osajoukkoon, eli jokaisen alkion tilan tallennukseen riittää yksi bitti.
Tästä eteenpäin bittitaulukot merkitään ilman välejä ja pilkkuja. Esimerkiksi viikonpäivien tallennuksessa bittitaulukot 0100000, 1110010 ja 0101001 tarkoittavat vastaavasti osajoukkoja {ti}, {ma, ti, ke, la} ja {ti, to, su}.
Esimerkki: Miten voitaisiin tallentaa vuorokauden tuntien osajoukko, ja miten esitettäisiin tilanne, jossa valittuna ovat ajat 8 - 12 ja 14 - 16?
Vastaus: Vuorokaudessa on 24 tuntia, joista jokainen voi olla vapaana tai valittuna. Osajoukko voidaan siis tallentaa 24 bitillä, yksi bitti jokaista tuntia kohden. Annetun tilanteen esitys olisi 000000001111001100000000.
Esimerkki: Taikaneliön jokaisella rivillä on neljä eri lukua väliltä 1 – 16. Miten voitaisiin tallentaa yhdellä rivillä olevien lukujen osajoukko, ja miten esitettäisiin tilanne, jossa rivillä ovat luvut 7, 2, 9 ja 16?
Vastaus: Valittavia lukuja on 16, joten osajoukko voidaan tallentaa 16 bitillä. Annetun tilanteen esitys olisi 0100001010000001. Tässä ei kiinnitetä huomiota lukujen järjestykseen rivillä, ja jokaista osajoukkoa vastaa 4! = 24 eri riviä. Tallennustapa on hieman tuhlaileva, koska tilaa olisi mille tahansa osajoukolle, mutta todellisuudessa osajoukossa on aina tasan neljä alkiota.
Osajoukon käsittely
Bittitaulukkona tallennettua osajoukkoa voidaan käsitellä hyvin tehokkaasti ohjelmointikielen bittioperaatioilla. Seuraavassa tutkitaan erikseen yleisimpiä bittioperaatioita ja niiden vaikutusta osajoukkoon. Bittisiirto ja operaatio "not" kohdistuvat yhteen bittijoukkoon, operaatiot "and", "or" ja "xor" taas kohdistuvat kahteen bittijoukkoon.
- Bittisiirto tarkoittaa, että kaikki bitit siirtyvät tietyn verran vasemmalle tai oikealle. Jos bittijoukkoa ajattelee positiivisena lukuna, yksi askel vasemmalle vastaa kertomista kahdella ja yksi askel oikealle vastaa jakamista kahdella (pyöristys alaspäin kokonaisluvuksi). Esimerkiksi kun bittejä 0001101 siirretään kaksi askelta vasemmalle, saadaan tulokseksi 0110100. Tyhjiksi jääneisiin kohtiin tulee aina nollabitti. Tämä vastaa kymmenjärjestelmän laskua 13 * 2 * 2 = 52. Bittisiirtoa voidaan käyttää osajoukon luonnissa aloittamalla osajoukosta, jonka ensimmäinen alkio on valittuna, ja siirtämällä valintaa oikealle haluttuun kohtaan. Esimerkiksi bitit 1000000 vastaavat viikonpäivien osajoukkoa {ma}, ja kun bittejä siirretään kolme askelta oikealle, saadaan 0001000 eli osajoukko {to}.
- Operaatio "not" muuttaa kaikki bitit päinvastaisiksi. Esimerkiksi jos bitit ovat alun perin 0110001, lopputulos on 1001110. Osajoukkoon kohdistettuna "not" tarkoittaa, että uuteen osajoukkoon tulevat kaikki alkiot, joita vanhassa ei ole. Esimerkiksi bitit 0110001 vastaavat viikonpäivien osajoukkoa {ti, ke, su}, ja operaation "not" seurauksena saadaan 1001110 eli osajoukko {ma, to, pe, la}.
- Operaatio "and" yhdistää kaksi bittijoukkoa. Jokaista bittiparia tutkitaan erikseen, ja jos kumpikin bitti on 1, tulokseen tulee 1, muuten 0. Esimerkiksi lähtöbiteistä 1101010 ja 0110010 saadaan tulokseksi 0100010. Kahteen osajoukkoon kohdistettuna "and" valikoi alkiot, jotka esiintyvät molemmissa osajoukoissa. Esimerkiksi bitit 1101010 ja 0110010 vastaavat viikonpäivien osajoukkoja {ma, ti, to, la} ja {ti, ke, la}. Operaation "and" tuloksena on 0100010, joten yhteiset päivät ovat {ti, la}. Näin voidaan myös tutkia, sisältyykö tietty osajoukko toiseen osajoukkoon.
- Operaatio "or" yhdistää kaksi bittijoukkoa. Jokaista bittiparia tutkitaan erikseen, ja jos kumpikin bitti on 0, tulokseen tulee 0, muuten 1. Esimerkiksi lähtöbiteistä 1101010 ja 0110010 saadaan tulokseksi 1111010. Kahteen osajoukkoon kohdistettuna "or" liittää yhteen kaikki osajoukoissa esiintyvät alkiot. Esimerkiksi bitit 1101010 ja 0110010 vastaavat viikonpäivien osajoukkoja {ma, ti, to, la} ja {ti, ke, la}. Operaation "or" tuloksena on 1111010, joten kaikki päivät ovat {ma, ti, ke, to, la}.
- Operaatio "xor" yhdistää kaksi bittijoukkoa. Jokaista bittiparia tutkitaan erikseen, ja jos biteillä on eri arvot, tulokseen tulee 1, muuten 0. Esimerkiksi lähtöbiteistä 0100111 ja 0010001 saadaan tulokseksi 0110110. Osajoukkoihin kohdistettuna "xor" muuttaa haluttujen alkioiden tilat päinvastaisiksi eli poistaa osajoukosta siihen kuuluvan alkion tai lisää osajoukkoon siihen kuulumattoman alkion. Esimerkiksi bitit 0100111 ja 0010001 vastaavat viikonpäivien osajoukkoja {ti, pe, la, su} ja {ke, pe}. Operaation "xor" tuloksena on 0110110, joka voidaan tulkita, että osajoukossa {ti, pe, la, su} muutetaan alkioiden {ke, pe} tilaa, jolloin tulos on {ti, ke, la, su}. Yhtä hyvin osajoukkojen roolit voisivat olla toisinpäin.
Esimerkki: Miten bittitaulukkona tallennetusta osajoukosta voidaan poistaa alkioita?
Vastaus: Tässä voidaan käyttää yhdessä operaatioita "not" ja "and". Muodostetaan ensin osajoukko, jossa on kaikki paitsi poistettavat alkiot, minkä jälkeen erotetaan osajoukkojen yhteiset alkiot. Esimerkiksi jos viikonpäivistä {ma, ke, to, pe} tulee poistaa {ke, pe}, osajoukot ovat 1011100 ja 0010100. Operaatiolla "not" jälkimmäisestä osajoukosta saadaan 1101011, ja operaatiolla "and" osajoukoista 1011100 ja 1101011 saadaan 1001000. Lopullinen osajoukko on siis {ma, to}.
Parhaassa tapauksessa koko osajoukko mahtuu yhteen muuttujaan. Esimerkiksi jos osajoukko valitaan 30 alkion joukosta, sen voi tallentaa yhteen 32-bittiseen muuttujaan. Jos ohjelmassa yhdistetään ja vertaillaan runsaasti osajoukkoja, tämä muutos voi nopeuttaa ohjelmaa merkittävästi. Yhtäkkiä vaivalloisen kahden taulukon läpikäynnin korvaa yksi ainoa nopea bittioperaatio.
Osajoukon käsittelystä bittitaulukkona on esimerkkiohjelmia C:lle, Pascalille ja QBasicille.
Projekti: Kirjoita ohjelma, joka laskee, kuinka monella tavalla kahdeksan kuningatarta voidaan asettaa shakkilaudalle niin, etteivät ne uhkaa toisiaan.
Projekti: Putkapostissa 9 väitetään, että tietynlaisia 4x4-taikaneliöitä olisi yhteensä 549504. Tarkista tämä tulos omalla ohjelmalla.
Numerointihaaste
Tutkitaan lopuksi peliä, joka tunnetaan muiden muassa nimillä "Klotski", "Forget-me-not" ja "L'Âne rouge". Pelin aloitustilanne näkyy kuvassa, ja tarkoitus on saada palikoita liikuttamalla suuri neliö ulos kehikosta. Mitään muita palikoita ei saa poistaa pelistä, vaan niiden täytyy pysyä kehikon sisällä.
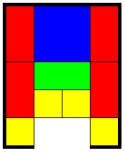
Kuinka monta bittiä tarvitset tämän pelin minkä tahansa tilanteen tallennukseen? (Yritä päästä alle 20 bittiin!)
Lopuksi
Ohjelmoinnissa ei yleensä kannata murehtia jokaista tuhlattua bittiä. Jos tieto mahtuu suoraan 12 bittiin, ei välttämättä kannata keksiä monimutkaista järjestelmää, jolla sen saa ahdettua 11 bittiin. Jopa yhden bitin totuusarvoja tallennetaan surutta 16 tai 32 bitin muuttujiin, joiden käsittely on usein bittiviritelmiä tehokkaampaa. Mutta toisinaan muutamasta bitistä voi olla kiinni, onko ohjelman toteutus ylipäänsä mahdollista käytössä olevassa ympäristössä.
Voit lähettää tästä oppaasta palautetta alla olevalla lomakkeella tai sähköpostilla osoitteeseen antti.laaksonen@ohjelmointiputka.net. Myös jos jokin asia jäi epäselväksi, voit kysyä tarkennusta asiaan. Kerro lisäksi, mitä aiheita tässä opassarjassa tai oppaissa yleensä kannattaisi käsitellä tulevaisuudessa.
Antti Laaksonen, 14.6.2007
- Edellinen opas
- Seuraava opas
Kommentit
lol eka xD
Toka :/
kolmas =D
en jaksanu lukee iha ajatuksella, mutta vaikuttaa hyvältä oppaalta :D
pitää kattoo joku kerta uudestaan läpi
Tommittaja [29.12.2008 21:32:01]
liikaa tietoa.. aivot sanoi sopimuksen irti..
Kirjoita kommentti
Huomio! Kommentoi tässä ainoastaan tämän oppaan hyviä ja huonoja puolia. Älä kirjoita muita kysymyksiä tähän. Jos koodisi ei toimi tai tarvitset muuten vain apua ohjelmoinnissa, lähetä viesti keskusteluun.