Oppaat: Algoritmien aakkoset: Osa 2 - Vaativuusluokkia
Kirjoittaja: Antti Laaksonen (2009).
Vaativuusluokka tarkoittaa, mikä funktio on O-merkinnän sisällä algoritmin aikavaativuudessa tai tilavaativuudessa. Keskiarvoalgoritmin tarkastelussa tulivat esille vaativuusluokat O(1) ja O(n), joissa funktiot ovat f(n) = 1 ja f(n) = n. Tässä oppaassa käsitellään lisää keskeisiä vaativuusluokkia ja luonnehditaan niitä vastaavia algoritmityyppejä. Melko pieni määrä vaativuusluokkia riittää monen algoritmin luokitteluun.
Tästä lähtien opassarjassa kiinnitetään huomiota lähinnä algoritmien aikavaativuuksiin ja tilavaativuudet jäävät taka-alalle. Tämä johtuu siitä, että algoritmin saaminen nopeaksi on tavallisesti ensisijainen tavoite eikä algoritmin tilankäyttö aiheuta yleensä ongelmia. Niinpä myös vaativuusluokat esitellään aikavaativuuksien näkökulmasta. Vaativuusluokkien esitysjärjestys on nopeimmasta hitaimpaan.
O(1) - vakioaikainen algoritmi
Vakioaikaisen algoritmin suoritus vie aina yhtä kauan aikaa riippumatta käsiteltävien tietojen määrästä. Tämä tarkoittaa, että algoritmissa ei saa olla silmukoita, joiden toistokertojen määrä vaihtelisi sen mukaan, miten paljon tietoa algoritmille annetaan. Vakioaikainen algoritmi on aikavaativuuden kannalta nopein mahdollinen algoritmi.
Vakioaikaiset algoritmit ovat harvinaisia, koska yleensä kaikki annetut tiedot täytyy käydä edes kerran läpi, jotta algoritmi voi ilmoittaa vastauksen luotettavasti. Esimerkiksi jos tehtävänä on laskea lukujen summa, algoritmi ei voi mitenkään saada summaa selville käymättä läpi kaikkia lukuja eikä vakioaikainen algoritmi tule tässä kysymykseen.
Esimerkki: Jos taulukossa on joukko lukuja, jotka on järjestetty pienimmästä suurimpaan, on olemassa vakioaikainen algoritmi, joka selvittää taulukon pienimmän luvun. Algoritmin täytyy vain katsoa, mikä luku on taulukon ensimmäisessä kohdassa, koska se on varmasti pienin, kun luvut ovat kerran järjestyksessä. Tähän kuluu sama aika riippumatta siitä, miten paljon lukuja koko taulukossa on.
O(log(n)) - logaritminen algoritmi
Logaritmifunktio log(n) (kantaluku 2) ilmoittaa, miten monta kertaa luku n täytyy puolittaa, jotta päästään lukuun 1. Esimerkiksi log(8) on 3, koska luku 8 täytyy puolittaa kolmesti, jotta tulos on 1. Joskus logaritmifunktion arvo on desimaaliluku: esim. log(20) on noin 4,32, koska jos luvun 20 puolittaa neljästi, tulos on noin 1,25, ja seuraava puolitus veisi jo luvun 1 alle.
Logaritminen algoritmi pystyy joka askeleella pienentämään ongelman koon puoleen, kunnes ongelma on niin pieni (noin 1), että sen ratkaisu on selvä. Tällainen algoritmi on todella nopea: vaikka luku n olisi suurikin, sitä ei tarvitse puolittaa kovin monta kertaa, ennen kuin tulos alittaa jo luvun 1. Esimerkiksi jos logaritmiselle algoritmille annetaan taulukko, jossa on miljoona lukua, algoritmi tarvitsee sen käsittelyyn vain noin 20 askelta, koska log(1000000) on noin 20.
Esimerkki: Jos taulukon luvut on järjestetty, on mahdollista tarkistaa logaritmisessa ajassa, onko tietty luku taulukossa. Algoritmin nimi on binäärihaku, ja sen toiminta muistuttaa nimen etsimistä puhelinluettelosta. Algoritmi pienentää hakualuetta joka vaiheessa puolella sen mukaan, onko jäljellä olevista luvuista keskimmäinen pienempi vai suurempi kuin etsittävä luku.
Seuraavassa kuvassa näkyy binäärihaun toiminta, kun taulukosta etsitään lukua 5:
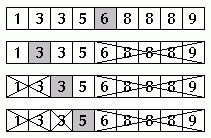
Taulukon keskimmäinen luku on 6, joka on suurempi kuin 5. Siis luku 5 ei voi esiintyä taulukossa puolenvälin jälkeen. Jäljellä olevan taulukon osan keskimmäinen luku on 3. Siis jos luku 5 on taulukossa, sen täytyy olla taulukon toisessa neljänneksessä. Jne.
O(n) - lineaarinen algoritmi
Lineaarinen algoritmi sisältää usein yhden for-silmukan, jossa annetut tiedot käydään läpi:
for i = 1 to n:
...Lineaarisen algoritmin ajankäyttö kasvaa samassa suhteessa kuin käsiteltävän tiedon määrä. Esimerkiksi algoritmi voi käydä läpi tiedot aina kolmeen kertaan tai aina puolet tiedoista. Lineaarinen algoritmi on aikavaativuuden kannalta nopein mahdollinen algoritmi, jos ongelma on luonteeltaan sellainen, että kaikki annetut tiedot täytyy joka tapauksessa tarkistaa.
Esimerkki: Jos taulukossa on lukuja, jotka eivät ole välttämättä järjestyksessä, on olemassa lineaarinen algoritmi, joka etsii taulukon pienimmän luvun. Algoritmi käy taulukon kaikki luvut läpi ja pitää kirjaa pienimmästä luvusta. Samoin on olemassa lineaarinen algoritmi, joka tarkistaa, onko tietty luku taulukossa. Algoritmi käy taulukon kaikki luvut läpi ja vertaa jokaista etsittävään lukuun.
O(n2) - neliöllinen algoritmi
Neliöllinen algoritmi sisältää usein kaksi sisäkkäistä for-silmukkaa:
for i = 1 to n:
for j = 1 to n:
...Neliöllinen algoritmi voi käydä läpi kaikki parit, jotka voidaan muodostaa annetuista tiedoista. Algoritmi voi siis verrata jokaista tietoa jokaiseen tietoon. Tällöin ensimmäinen silmukka valitsee ensimmäisen tiedon ja toinen silmukka valitsee toisen tiedon.
Esimerkki: Jos taulukossa on joukko lukuja, on olemassa neliöllinen algoritmi, joka tarkistaa, onko taulukossa kahta samaa lukua. Algoritmin ensimmäinen silmukka käy läpi taulukossa olevat luvut ja toinen silmukka tarkistaa, esiintyykö käsiteltävä luku jossain toisessa taulukon kohdassa.
O(n3) - kuutiollinen algoritmi
Kuutiollinen algoritmi sisältää usein kolme sisäkkäistä for-silmukkaa:
for i = 1 to n:
for j = 1 to n:
for k = 1 to n:
...Vastaavasti kuin neliöllinen algoritmi voi käydä läpi kaikki parit, kuutiollinen algoritmi voi käydä läpi kaikki kolmikot, jotka voidaan muodostaa annetuista tiedoista.
Esimerkki: Jos taulukossa on joukko lukuja, on olemassa kuutiollinen algoritmi, joka tarkistaa, voiko taulukosta valita luvut a, b ja c niin, että a + b = c. Ensimmäinen silmukka valitsee luvun a, toinen silmukka valitsee luvun b ja kolmas silmukka valitsee luvun c. Silmukoiden sisällä tarkistetaan, päteekö todella a + b = c.
O(nk) - polynominen algoritmi
Yleisemmin vaativuusluokkaan O(nk) kuuluvan polynomisen algoritmin yksi tulkinta on, että siinä on k sisäkkäistä for-silmukkaa. Luku k ei ole käytännössä yleensä kovin suuri: jos esim. vaativuusluokka olisi O(n17), algoritmissa olisi 17 sisäkkäistä for-silmukkaa, mutta on vaikeaa kuvitella ongelmaa, jonka ratkaisu vaatisi tietojen määrästä riippumatta nimenomaan 17 sisäkkäistä for-silmukkaa.
Kaikki tähän mennessä esitellyt vaativuusluokat ovat olleet korkeintaan polynomisia. Jos ongelman ratkaisuun on keksitty polynominen algoritmi, tästä voi olla tyytyväinen, koska polynomiset algoritmit ovat melko nopeita (ellei k ole liian suuri). Kuitenkin on monia ongelmia, joihin ei tunneta polynomista algoritmia.
O(kn) - eksponentiaalinen algoritmi
Eksponentiaalisen algoritmin suoritus voi haarautua joka tiedon kohdalla k osaan. Esimerkiksi jos algoritmin aikavaativuus on O(2n), algoritmin suoritus voi haarautua n kertaa kahteen osaan. Eksponentiaalinen algoritmi on todella hidas, ellei n ole pieni, koska jokainen haarautuminen kasvattaa algoritmin työmäärää räjähdysmäisesti.
Polynomisissa algoritmeissa for-silmukoiden määrä on kiinteä ja niiden yläraja vaihtelee tiedon määrän mukaan. Vastaavasti eksponentiaalisissa algoritmeissa "for-silmukoiden" määrä vaihtelee tiedon määrän mukaan ja niiden yläraja on kiinteä. Esimerkiksi jos algoritmin aikavaativuus on O(2n), siinä on n "for-silmukkaa", joista jokainen käy läpi kaksi lukua. Käytännössä koodiin ei voi kirjoittaa vaihtuvaa määrää for-silmukoita vaan täytyy käyttää esim. rekursiota, josta kerrotaan lisää myöhemmissä oppaissa.
Esimerkki: Jos taulukossa on joukko lukuja, on olemassa eksponentiaalinen algoritmi, joka etsii tavan jakaa luvut kahteen ryhmään niin, että ryhmien lukujen summat ovat mahdollisimman lähellä toisiaan. Algoritmi haarautuu joka luvun kohdalla kahden mahdollisuuden mukaan: joko luku menee ryhmään A tai sitten se menee ryhmään B. Algoritmi pitää kirjaa ryhmien summista sekä pienimmän erotuksen tuottavista jaoista. Algoritmi haarautuu kahteen osaan joka luvun kohdalla, joten algoritmin aikavaativuus on O(2n).
Seuraavassa kuvassa näkyy algoritmin toiminta, kun taulukossa ovat luvut 7, 3, 2 ja 9.
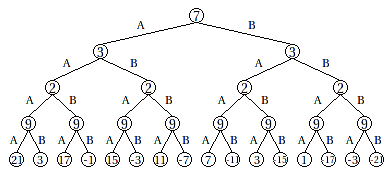
Alimmalla rivillä näkyy ryhmän A lukujen summan ja ryhmän B lukujen summan erotus. Esimerkiksi kun ryhmään A valitaan luvut 7, 2 ja 9 ja ryhmään B valitaan luku 3, ryhmän A lukujen summa on 18 ja ryhmän B lukujen summa on 3, joten erotus on 15. Jos ryhmään A valitaan luvut 7 ja 3 ja ryhmään B valitaan luvut 2 ja 9 (tai vastaavasti toisinpäin), summat eroavat toisistaan vain yhdellä, ja tämä on paras mahdollinen jakotapa.
Kasvunopeudet
Jos käsiteltävien tietojen määrä kasvaa yhdellä, muut esitellyt algoritmityypit toimivat lähes yhtä nopeasti kuin ennenkin, mutta eksponentiaalisen algoritmin ajankäyttö k-kertaistuu. Edellisessä esimerkissä jos taulukkoon tulee uusi luku, mahdollisia jakotapoja on 32 aiemman 16:n sijasta eli aika kaksinkertaistuu.
Jos käsiteltävien tietojen määrä kaksinkertaistuu,
- vakioaikaisen algoritmin nopeus ei muutu,
- logaritminen algoritmi tarvitsee yhden lisäaskeleen,
- lineaarinen algoritmi tarvitsee kaksinkertaisen ajan,
- neliöllinen algoritmi tarvitsee nelinkertaisen ajan,
- kuutiollinen algoritmi tarvitsee kahdeksankertaisen ajan,
- O(nk)-aikainen algoritmi tarvitsee 2k-kertaisen ajan ja
- eksponentiaalisen algoritmin ajankäyttö kasvaa räjähdysmäisesti.
Vaativuuksien yhdistys
Jos algoritmissa on monta vaihetta, joilla on tietyt aikavaativuudet, kokonaisaikavaativuus on niistä suurin. Esimerkiksi jos algoritmin vaiheiden aikavaativuudet ovat O(n), O(n2) ja O(1), algoritmin kokonaisaikavaativuus on O(n2). Tämä johtuu siitä, että muiden vaiheiden merkitys työläimpään vaiheeseen verrattuna on mitätön.
Jos algoritmissa on sisäkkäin vaiheita, joilla on tietyt aikavaativuudet, kokonaisaikavaativuus on aikavaativuuksien tulo. Esimerkiksi jos algoritmi käy kaikki tiedot läpi (O(n)) ja suorittaa jokaisen kohdalla binäärihaun (O(log(n))), kokonaisaikavaativuus on O(n * log(n)).
Monta muuttujaa
Joskus algoritmin käsiteltävien tietojen määrää kuvaa luontevasti monta muuttujaa, joilla on eri vaikutus vaativuuksiin. Esimerkiksi jos algoritmille annetaan taulukko, jossa on n riviä ja m saraketta ja algoritmi käy koko taulukon läpi, aikavaativuus on O(n * m). Toisaalta jos algoritmi käy kaikki rivit läpi ja suorittaa joka rivillä binäärihaun sarakkeiden suuntaisesti, aikavaativuus on O(n * log(m)).
Nopeuden arviointi
Algoritmin aikavaativuus kertoo, kuinka monta kertaa suunnilleen algoritmi tekee jonkin yksinkertaisen asian. Esimerkiksi polynomisissa algoritmeissa for-silmukoiden sisällä olevan koodin suoritus on yksinkertainen asia. Jos aikavaativuus on O(n2) ja n on 50, algoritmi tekee noin 502 = 2500 kertaa jotain yksinkertaista.
Toisaalta voidaan arvioida, kuinka monta kertaa sekunnissa tietokone ehtii tehdä jonkin yksinkertaisen asian. Jos yksinkertainen asia on muutaman rivin koodi, nykyaikainen tietokone ehtii tehdä sen ehkä sata miljoonaa kertaa sekunnissa. Jos yksinkertainen asia on työläämpi, nykyaikainen tietokone ehtii tehdä sen ehkä kymmenen miljoonaa kertaa sekunnissa. Nämä arviot ovat karkeita, mutta tärkeää on suuruusluokka: sekunnissa ehtii tehdä miljoonia yksinkertaisia asioita, selvästi enemmän kuin tuhansia mutta selvästi vähemmän kuin biljoonia.
Seuraavaan taulukkoon on koottu, miten suuren tietomäärän (n:n arvo) eri aikavaativuuksia edustavat algoritmit ehtivät käsitellä, jos tietokone ehtii tehdä yksinkertaisen asian kymmenen miljoonaa kertaa sekunnissa ja algoritmi saa käyttää aikaa sekunnin, minuutin, tunnin, päivän tai vuoden. Vakioaikainen ja logaritminen algoritmi ehtivät käsitellä jo sekunnissa minkä tahansa käytännössä järkevän tietomäärän.
| aikaraja | O(n) | O(n * log(n)) | O(n2) | O(n3) | O(2n) | O(3n) |
|---|---|---|---|---|---|---|
| sekunti | 10 miljoonaa | 500000 | 3000 | 200 | 23 | 15 |
| minuutti | 600 miljoonaa | 25 miljoonaa | 25000 | 850 | 29 | 18 |
| tunti | 35 miljardia | miljardi | 200000 | 3000 | 35 | 22 |
| päivä | 850 miljardia | 25 miljardia | miljoona | 10000 | 40 | 25 |
| vuosi | 300000 miljardia | 7000 miljardia | 20 miljoonaa | 70000 | 48 | 30 |
Nämä tulokset tukevat väitettä, että polynomiset algoritmit ovat nopeita verrattuna eksponentiaalisiin. Vaikka eksponentiaalinen algoritmi saisi vuoden suoritusaikaa, se ei ehtisi käsitellä edes n:n arvoa 50. Eli jos tehtävänä olisi jakaa luvut tasaisesti kahteen ryhmään ja käytettäisiin annettua eksponentiaalista algoritmia, aikaa kuluisi yli vuosi, jos lukuja olisi 50.
Eksponentiaalisten algoritmien ongelma on, että jos tietoa on paljon, vastaus ei tule valmiiksi, vaikka odottaisi miten kauan (ihmisiän). Ikävä kyllä moniin ongelmiin tunnetaan vain eksponentiaalisia tai yhtä hitaita algoritmeja. Välillä kuitenkin algoritmi on käytännössä nopea, vaikka se voi olla pahimmassa tapauksessa eksponentiaalinen. Joskus taas voidaan käyttää arviointialgoritmia, joka ei löydä aina tarkkaa vastausta mutta joka toimii nopeasti.
Toisaalta myös polynomisten algoritmien välillä on merkittäviä eroja. Jos käsiteltävänä on kymmenen tuhatta lukua ja algoritmin aikavaativuus on O(n3), vastausta täytyy odottaa noin päivä, mikä on usein kohtuuton odotusaika. Jos algoritmin aikavaativuus onkin O(n2), vastaus valmistuu alle minuutissa, mikä on paljon siedettävämpi nopeus. Jos taas algoritmin aikavaativuus on O(n), algoritmi ilmoittaa vastauksen silmänräpäyksessä.
Antti Laaksonen, 24.4.2009
- Edellinen opas
- Seuraava opas
Kommentit
Loistavaa! Tätä olen etsinytkin.
Kiitoksia.
Hyvä taulukko. Minua kiinnostaa, miten olet sen tehnyt.
Toisin sanoen miten olet päätellyt että O(n)=10M sekunnissa?
Antti Laaksonen [30.06.2009 09:44:12]
Olen ensinnäkin olettanut, että tietokone pystyy tekemään kymmenen miljoonaa yksinkertaista asiaa sekunnissa.
Sitten esimerkiksi sekuntirivi saadaan laskemalla n näistä kaavoista:
n = 10000000
n*log(n) = 10000000
n^2 = 10000000
n^3 = 10000000
2^n = 10000000
3^n = 10000000
Vastaavasti minuuttirivi saadaan laskemalla n näistä kaavoista:
n = 10000000 * 60
n*log(n) = 10000000 * 60
n^2 = 10000000 * 60
n^3 = 10000000 * 60
2^n = 10000000 * 60
3^n = 10000000 * 60
Minusta O-notaatio on hämärä ja epäselvä. Kts. nimimerkin fedja mielipide osoitteessa http://www.artofproblemsolving.com/Forum/
Kirjoita kommentti
Huomio! Kommentoi tässä ainoastaan tämän oppaan hyviä ja huonoja puolia. Älä kirjoita muita kysymyksiä tähän. Jos koodisi ei toimi tai tarvitset muuten vain apua ohjelmoinnissa, lähetä viesti keskusteluun.