Oppaat: Algoritmien aakkoset: Osa 1 - Aikavaativuus ja tilavaativuus
- Osa 1 - Aikavaativuus ja tilavaativuus
- Osa 2 - Vaativuusluokkia
Kirjoittaja: Antti Laaksonen (2009).
Tämän opassarjan tarkoituksena on antaa yleiskäsitys algoritmien suunnittelusta ja niiden tehokkuuden arvioinnista. Oppaat on kirjoitettu olettaen, että ohjelmoinnin peruskäsitteet – muuttujat, taulukot, ehtolauseet (if), silmukat (for, while) ja aliohjelmat – ovat lukijalle tuttuja. Käytetyllä ohjelmointikielellä ei ole merkitystä, vaan opassarjan asiat pätevät kaikissa ohjelmointikielissä.
Mikä on algoritmi?
Algoritmi on tarkasti kuvattu toimintaohje, joka ratkaisee jonkin ongelman annettujen lähtötietojen perusteella. Kun algoritmin jokainen vaihe on ilmoitettu yksiselitteisesti, se soveltuu tietokoneen suoritettavaksi. Tietokoneen vahvuuksia ovat nopeus ja tarkkuus: tietokone pystyy suorittamaan sekunnissa miljoonia yksinkertaisia toimintoja virheettömästi.
Esimerkiksi jos on annettu joukko lukuja, niiden keskiarvon voi laskea seuraavalla algoritmilla:
- Laske kaikki luvut yhteen.
- Jaa tulos lukujen määrällä.
Jos luvut ovat 4, 8 ja 3, algoritmi antaa vastaukseksi (4 + 8 + 3) / 3 = 5.
Tässä on sama algoritmi tietokoneen ymmärtämässä muodossa:
summa = 0
for i = 1 to maara:
summa = summa + luvut[i]
keskiarvo = summa / maaraAlgoritmien merkitys
Esimerkiksi seuraaviin ongelmiin tarvitaan hyviä algoritmeja. Näihin ongelmiin palataan opassarjan kuluessa.
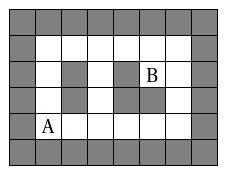
Mikä on lyhin reitti labyrintissä pisteestä A pisteeseen B?
Mikä on merkkijonossa olevan laskun tulos? Esimerkiksi jos merkkijono on "25 - (4 + 2) * 3", tulos on 7.
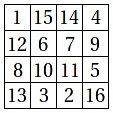
Miten voi muodostaa taikaneliön, joka sisältää luvut 1...n ja jossa jokaisen rivin, sarakkeen ja lävistäjän summa on sama?
Algoritmin ajankäyttö
Samaan ongelmaan on usein olemassa monia algoritmeja, joiden nopeus voi vaihdella huomattavasti. Usein ei vielä riitä, että ongelmaan keksii toimivan algoritmin, vaan haaste on siinä, että algoritmin täytyy olla riittävän nopea. Vaikka tietokone on hyvin nopea, senkin nopeudella on rajansa.
Jos ongelman ratkaiseva algoritmi on hidas, maailman tehokkain tietokone voi tarvita sen suoritukseen miljardeja vuosia. Monien ongelmien ratkaisuun ei tunneta mitään nopeaa algoritmia. Joidenkin ongelmien ratkaisuun ei tunneta edes mitään hidasta algoritmia.
Algoritmin tilankäyttö
Algoritmin nopeuden lisäksi on kiinnostavaa, miten paljon muistia algoritmi tarvitsee välitulosten yms. tallennukseen. Jos algoritmi tarvitsee paljon muistia lähtötietojen lisäksi, tämä on algoritmin heikkous. Tietokoneessa on paljon muistia, mutta sitä ei ole rajattomasti.
Pyrkimys saada sekä algoritmin ajankäyttö että tilankäyttö pieneksi voi viedä algoritmin suunnittelua vastakkaisiin suuntiin. Välillä algoritmin saa nopeaksi juuri käyttämällä paljon muistia.
O-merkintä
Algoritmin ajankäyttöön ja tilankäyttöön vaikuttavat mm. käytettävän tietokoneen ominaisuudet, käytettävä ohjelmointikieli ja pienet yksityiskohdat algoritmin toteutuksessa. Tämän vuoksi ajankäytön ja tilankäytön tarkka arviointi etukäteen on vaikeaa.
O-merkinnän tarkoituksena on antaa yleiskuva algoritmin toiminnasta: miten algoritmin käsittelemän tiedon määrä vaikuttaa sen ajankäyttöön ja tilankäyttöön. Jos algoritmin pitää käsitellä enemmän tietoa, se muuttuu yleensä hitaammaksi ja muistia kuluu enemmän. Algoritmien erot liittyvät siihen, miten voimakkaita muutokset ovat.
Esimerkiksi on mahdollista, että algoritmit A, B ja C vievät kukin 5 millisekuntia aikaa, kun niille annetaan 10 lukua. Mutta jos lukuja onkin 20, A:n suoritus voi kestää 8 millisekuntia, B:n 3 tuntia ja C:n 35 vuotta. O-merkintä tuo esiin tällaisia eroja algoritmien toiminnassa.
Algoritmin aikavaativuus
Algoritmin aikavaativuus on O(f(n)), jos algoritmin ajankäyttö kasvaa samassa suhteessa tai hitaammin kuin funktio f(n), kun muuttuja n kuvaa tiedon määrää. Toisin sanoen algoritmin suoritus vie aikaa korkeintaan k * f(n) jollain vakiolla k, kun n on riittävän suuri.
Keskiarvoalgoritmi viettää suurimman osan ajasta for-silmukassa, jossa lasketaan lukujen summa. Jos lukujen määrä on n, for-silmukan sisällä oleva koodi suoritetaan n kertaa. Lopussa oleva jakolasku suoritetaan aina kerran lukujen määrästä riippumatta, ja sen vaikutus kokonaisuuteen on mitätön.
Keskiarvoalgoritmin aikavaativuus on O(n) (eli f(n) = n). Tämä tarkoittaa, että algoritmin ajankäyttö on suoraan verrannollinen lukujen määrään. Jos lukujen määrä kaksinkertaistuu, algoritmin täytyy laskea yhteen kaksinkertainen määrä lukuja, jolloin aikaa kuluu kaksinkertaisesti.
Algoritmin tilavaativuus
Algoritmin tilavaativuus on O(f(n)), jos algoritmin tilankäyttö kasvaa samassa suhteessa tai hitaammin kuin funktio f(n), kun muuttuja n kuvaa tiedon määrää. Toisin sanoen algoritmi vie tilaa korkeintaan k * f(n) jollain vakiolla k, kun n on riittävän suuri.
Keskiarvoalgoritmi varaa kolme apumuuttujaa, joista yhteen lasketaan lukujen summa, toinen on for-silmukan laskurimuuttuja ja kolmanteen lasketaan lopuksi lukujen keskiarvo. Muuttujien määrä on sama riippumatta lukujen määrästä. Vaikka lukuja olisi miljoona, silti kolme muuttujaa riittää.
Keskiarvoalgoritmin tilavaativuus on O(1) (eli f(n) = 1). Tämä tarkoittaa, että lukujen määrä ei vaikuta algoritmin tilankäyttöön. Jos lukujen määrä kaksinkertaistuu, algoritmi ei tarvitse yhtään enempää muistia.
O-merkinnän tulkinta
O-merkintä antaa ylärajan algoritmin ajankäytölle tai tilankäytölle. Yläraja ei ole yksikäsitteinen, vaan samalle algoritmille voi antaa monta eri ylärajaa. Esimerkiksi keskiarvoalgoritmin tilavaativuus on myös O(n): muistinkäyttö on aina sama, joten se kasvaa varmasti korkeintaan samassa suhteessa lukujen määrän kanssa.
Yleensä O-merkinnän sisällä oleva funktio valitaan niin, että sen antama yläraja on melko tarkka. O-merkintä on nimittäin tiivistetty mainosteksti, joka kertoo, mihin algoritmi pystyy. Jos auton huippunopeus on 200 km/h, ei kannata mainostaa, että auton huippunopeus on 100 km/h, vaikka ostaja ei varmasti pettyisi. Samalla tavalla algoritmin suoritusaikaa tai muistinkäyttöä ei kannata väittää kohtuuttoman suureksi.
Antti Laaksonen, 24.4.2009
- Edellinen opas
- Seuraava opas
Kommentit
Hieno opas! Helpottaa varmasti monia.
"Näihin ongelmiin palataan opassarjan kuluessa."
Odottelen innolla.
Lähteet olisi hyvä lisätä.
Aiheesta lisää seuraavassa kirjassa noin sivulla 50
Vaikka keskiarvon laskeva menetelmä ei tarvitsekaan kuin 3 vakiokokoista muuttujaa, niin sen syötteenä olevat luvut vievät mittansa verran tilaa. Eli mikä tahansa keskiarvomenetelmää käyttävä suorituskelpoinen ohjelma vaatii tämän tilan, joten voisi sanoa, että keskiarvomenetelmänkin tilavaatimus on lineaarinen.
Voisi sanoa, että mikä tahansa ohjelma tahi algoritmi vaatii vähintään syötteensä koon verran tilaa. Tosin jotkin (ns. online-algoritmit) lukevat syötettä alkio kerrallaan, eikä niitä tarvitse välttämättä kirjoittaa talteen. Keskiarvonkin voi laskea "online-tyylisesti" kunhan muistaa jo lasketun keskiarvon ja jo laskettujen lukujen lukumäärän.
Hietamies, eiköhän oppaassa tarkoiteta juuri tuota, minkä itsekin tajusit: esimerkiksi lämpötila-anturin antamien lukujen keskiarvoja voidaan laskea reaaliajassa niin, että muistissa ei ole koskaan kuin yksi syötearvo (nykyinen lukema) sekä aiempien arvojen summa ja lukumäärä.
Kirjoita kommentti
Huomio! Kommentoi tässä ainoastaan tämän oppaan hyviä ja huonoja puolia. Älä kirjoita muita kysymyksiä tähän. Jos koodisi ei toimi tai tarvitset muuten vain apua ohjelmoinnissa, lähetä viesti keskusteluun.