Oppaat: Ohjelmoijan matematiikka: Osa 2 - Pituus ja kulma
Kirjoittaja: Antti Laaksonen (2007).
Tässä oppaassa tutkitaan erilaisia kolmioita, niiden sivujen pituuksia ja kulmien suuruuksia. Oppaan tärkeimmät asiat ovat Pythagoraan lause ja trigonometriset funktiot sini, kosini ja tangentti. Lisäksi oppaassa kerrotaan, kuinka trigonometriset funktiot liittyvät ympyrään ja miten ohjelmoija voi soveltaa niitä erilaisissa graafisissa ohjelmissa.
Pythagoraan lause
Suorakulmaisen kolmion muodostavat kaksi kateettia, joiden välillä on suora kulma, sekä hypotenuusa. Seuraavassa kuvassa sivut a ja b ovat kateetteja ja sivu c on hypotenuusa.
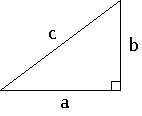
Pythagoraan lause liittää suorakulmaisen kolmion sivujen pituudet toisiinsa: kun kateettien pituudet korotetaan toiseen potenssiin ja lasketaan yhteen, saadaan tulokseksi hypotenuusan pituus korotettuna toiseen potenssiin. Matemaattisesti lause merkitään a2 + b2 = c2.
Kun suorakulmaisen kolmion sivujen pituuksista tunnetaan kaksi, voidaan Pythagoraan lauseen avulla laskea myös kolmannen pituus.
Esimerkki: Suorakulmaisen kolmion kateettien pituudet ovat 3 ja 4. Mikä on hypotenuusan pituus?
Vastaus: a = 3 ja b = 4. 32 + 42 = c2. c2 = 9 + 16 = 25. c = √25 = 5. Siis hypotenuusan pituus on 5.
Esimerkki: Suorakulmaisen kolmion toisen kateetin pituus on 12 ja hypotenuusan pituus on 13. Mikä on toisen kateetin pituus?
Vastaus: a = 12 ja c = 13. 122 + b2 = 132. b2 = 169 - 144 = 25. b = √25 = 5. Siis toisen kateetin pituus on 5.
Kahden pisteen etäisyys
Pythagoraan lauseen sovellus on kahden ruudukossa olevan pisteen etäisyyden laskeminen. Ruudukon pisteet voidaan kuvitella suorakulmaisen kolmion kärkipisteiksi, jolloin tämän kolmion hypotenuusan pituus on yhtä suuri kuin pisteiden etäisyys. Kun pisteiden koordinaatit tunnetaan, kateettien pituuksien laskeminen on helppoa.
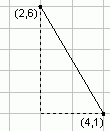
Pisteiden etäisyys vaakasuunnassa on 4 - 2 = 2, ja pisteiden etäisyys pystysuunnassa on 6 - 1 = 5. Nämä vastaavat suorakulmaisen kolmion kateettien pituuksia, joten 22 + 52 = c2. Edelleen c2 = 4 + 25 = 29 ja c = √29 ≈ 5,39, joka on pisteiden etäisyys.
Kun kahden pisteen koordinaatit ovat (x1, y1) ja (x2, y2), niiden etäisyys on yleisesti √(x2 - x1)2 + (y2 - y1)2.
Esimerkki: Kahden pisteen koordinaatit ovat (-2, 7) ja (6, 6). Kuinka kaukana pisteet ovat toisistaan?
Vastaus: √(6 + 2)2 + (6 - 7)2 = √64 + 1 = √65 ≈ 8,06.
Kulman ilmoitus
Tavalliset kulman yksiköt ovat aste ja radiaani. 180 astetta on π radiaania. (π ≈ 3,14159.)
Seuraavia kaavoja voi käyttää kulmien muutoksiin:
aste = (radiaani * 180) / π
radiaani = (aste / 180) * π
Esimerkki: Kuinka monta radiaania on 45 astetta?
Vastaus: (45 / 180) * π = (1 / 4) * π. Siis noin 0,79 radiaania.
Esimerkki: Kuinka monta astetta on 1 radiaani?
Vastaus: (1 * 180) / π = 180 / π. Siis noin 57 astetta.
Kolmion kulmat
Suorakulmaisen kolmion yksi kulma on tietysti 90 astetta. Mutta kuinka suuri on kuvassa kulma α?
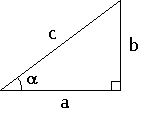
Trigonometriset funktiot sini, kosini ja tangentti liittyvät suorakulmaiseen kolmioon näin:
sin(α) = b / c
cos(α) = a / c
tan(α) = b / a
Sini on kulman vastaisen kateetin ja hypotenuusan suhde. Kosini on kulman viereisen kateetin ja hypotenuusan suhde. Tangentti on kulman vastaisen kateetin ja viereisen kateetin suhde. Näiden funktioiden avulla voidaan laskea mikä tahansa suorakulmaisen kolmion kulma, kun kahden sivun pituus tunnetaan.
Kun tiedetään kulman sini, kosini tai tangentti, varsinainen kulma voidaan laskea käänteisfunktioilla arkussini, arkuskosini ja arkustangentti. Esimerkiksi kun sin(α) = 0,62, α on arcsin(0,62) ≈ 38°. Trigonometristen funktioiden laskuun ei ole yksinkertaista tapaa, vaan avuksi tarvitaan laskinta tai tietokonetta.
Esimerkki: Kuinka suuri kuvan kulma α on, kun a = 3 ja c = 5?
Vastaus: cos(α) = 3 / 5. Siis α = arccos(3 / 5) ≈ 53°.
Esimerkki: Suorakulmaisen kolmion kateettien pituudet ovat 4 ja 7. Laske kolmion kulmien suuruudet.
Vastaus: Yksi kulma on 90°. Kun toinen kulma on α, tan(α) = 4 / 7. Siis α = arctan(4 / 7) ≈ 30°. Kolmion kulmien summa on 180°, joten kolmas kulma on 60°.
Muistikolmiot
Tässä on kaksi yleistä suorakulmaista kolmiota:
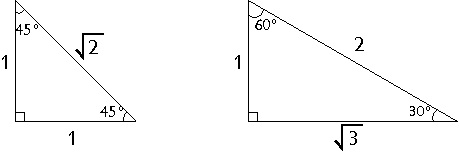
Näiden muistikolmioiden avulla voi ratkaista nopeasti monta laskua. Jos kolmion kulmat ovat samat kuin muistikolmiossa, myös sen sivujen pituudet ovat samassa suhteessa.
Esimerkki: Kolmion kulmat ovat 30°, 60° ja 90°. Hypotenuusan pituus on 6. Laske kateettien pituudet.
Vastaus: Kolmion sivujen pituudet ovat kuvaan verrattuna kolminkertaisia. Siis kateettien pituudet ovat 3 ja 3√3.
Näiden kolmioiden avulla voidaan määrittää joitakin trigonometristen funktioiden arvoja tarkasti:
| asteet | radiaanit | sini | kosini | tangentti |
|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 0 |
| 30 | π / 6 | 1 / 2 | √3 / 2 | √3 / 3 |
| 45 | π / 4 | √2 / 2 | √2 / 2 | 1 |
| 60 | π / 3 | √3 / 2 | 1 / 2 | √3 |
| 90 | π / 2 | 1 | 0 | - - |
Esimerkki: Kuinka suuri on kulma α, kun tan(α) = √3?
Vastaus: Taulukko kertoo: 60°.
Sinilause ja kosinilause
Tähän mennessä esitetyt tavat kolmion sivujen pituuksien ja kulmien laskentaan soveltuvat vain suorakulmaisiin kolmioihin. Nyt tulee kaksi yleisempää lausetta, joita voi käyttää kaikenlaisten kolmioiden kanssa.
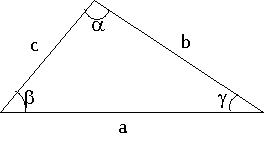
Sinilauseen mukaan kolmion jokaisen sivun ja sille vastakkaisen kulman sinin suhde on sama.
a / sin(α) = b / sin(β) = c / sin(γ)
Kosinilause on laajennettu Pythagoraan lause, joka pätee kaikilla kolmioilla.
a2 = b2 + c2 - 2 * b * c * cos(α)
Sivujen ja kulmien nimet täytyy valita yllä olevan kuvan mukaisesti, jotta lauseet pätevät.
Esimerkki: Kuvan kolmiossa a = 10, b = 8 ja c = 7. Laske kolmion kulmien suuruudet.
Vastaus: Kosinilauseen mukaan 102 = 82 + 72 - 2 * 8 * 7 * cos(α). Siis -2 * 8 * 7 * cos(α) = 102 - 82 - 72. -112 * cos(α) = 100 - 64 - 49. cos(α) = 13 / 112. Näin α on 83°. Sinilauseen mukaan 10 / sin(α) = 8 / sin(β). Siis sin(β) = sin(α) * 8 / 10, jolloin β on 53°. Kolmion kulmien summa on 180°, joten γ = 180° - 83° - 53° = 44°.
Kolmion pinta-ala
Kolmion pinta-ala on (kanta * korkeus) / 2, joten suorakulmaisen kolmion pinta-ala on (a * b) / 2, kun a ja b ovat kateettien pituudet.
Kolmion pinta-ala on myös (a * b * sin(γ)) / 2, jossa a ja b ovat kolmion kaksi sivua ja γ on niiden välissä oleva kulma.
Kolmas tapa kolmion pinta-alan laskuun on Heronin kaava. Kolmion pinta-ala on √n * (n - a) * (n - b) * (n - c), kun a, b ja c ovat kolmion sivujen pituudet ja n on puolet sivujen pituuksien summasta.
Esimerkki: Laske edellisen esimerkin kolmion pinta-ala.
Vastaus: a = 10, b = 8 ja γ = 44°. Siis pinta-ala on (10 * 8 * sin(44°)) / 2 ≈ 28.
Vastaus: n = (10 + 8 + 7) / 2 = 12,5. a = 10, b = 8 ja c = 7. Siis pinta-ala on √12,5 * (12,5 - 10) * (12,5 - 8) * (12,5 - 7) ≈ 28.
Yksikköympyrä
Yksikköympyrä on ympyrä, jonka säde on 1. Etäisyys ympyrän keskipisteestä sen kehälle on siis 1.
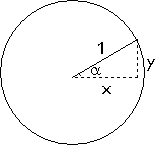
Kun liikutaan ympyrän keskipisteestä kehälle suuntaan α, kulman kosini ilmoittaa, kuinka paljon liikutaan vaakasuunnassa, ja kulman sini ilmoittaa, kuinka paljon liikutaan pystysuunnassa. Sopimuksen mukaan kulma ilmoittaa suunnan niin, että 0° osoittaa oikealle ja kulman suuruus kasvaa vastapäivään. Vastaavasti 90° osoittaa ylös, 180° osoittaa vasemmalle ja 270° osoittaa alas.
Kaikki ympyrän kehän pisteet voidaan laskea seuraavien kaavojen avulla:
x = cos(α)
y = sin(α)
Esimerkki: Laske ympyrän kehäpisteen sijainti, kun kulma on 20°.
Vastaus: x = cos(20°) ≈ 0,94. y = sin(20°) ≈ 0,34. Kehälle päästään siis liikkumalla 0,94 oikealle ja 0,34 ylös.
Esimerkki: Laske ympyrän kehäpisteen sijainti, kun kulma on 140°.
Vastaus: x = cos(140°) ≈ -0,77. y = sin(140°) ≈ 0,64. Kehälle päästään siis liikkumalla 0,77 vasemmalle ja 0,64 ylös.
Kosini ja sini palauttavat aina arvon väliltä -1..1. Kun kulma on 0°, kosini on 1 ja sini on 0. Kun kulma on 90°, kosini on 0 ja sini on 1. Kun kulma on 180°, kosini on -1 ja sini on 0. Kun kulma on 270°, kosini on 0 ja sini on -1. Kun kulma on 360°, kosini on 1 ja sini on 0.
Samat kosinit ja sinit kertautuvat 360 asteen välein. Esimerkiksi sin(1000°) on sama kuin sin(280°), koska 280° + 360° + 360° = 1000°. Myös sin(-80°) on sama kuin sin(280°), koska -80° + 360° = 280°. Koko ympyrän kierrokset eivät siis vaikuta sinin ja kosinin arvoon.
Kahdella eri kulmalla voi myös olla sama kosini tai sini. Kuvasta huomataan, että cos(α) = cos(-α) ja sin(α) = sin(180° - α). Lisäksi Pythagoraan lauseen perusteella cos(α)2 + sin(α)2 = 1.
Avaruusaluksen liike
Avaruusalus on ruudukon kohdassa (3, 4) ja se liikkuu suuntaan 115°. Sekunnissa avaruusalus liikkuu yhden ruudunmitan eteenpäin. Missä kohdassa avaruusalus on sekunnin ja viiden sekunnin kuluttua?
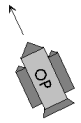
Sekunnin kuluttua avaruusalus on kohdassa (3 + cos(115°), 4 + sin(115°)) eli (2,58; 4,91). Viiden sekunnin kuluttua avaruusalus on kohdassa (3 + cos(115°) * 5, 4 + sin(115°) * 5) eli (0,87; 8,53).
Ohjelmoija voi usein ajatella näin: Kosini ja sini ilmoittavat, kuinka paljon jokin liikkuu vaaka- ja pystysuuntaan, kun kokonaissuunta on annettu ja kokonaismatka on 1. Jos kokonaismatka on muu kuin 1, vaaka- ja pystysuuntainen matka kerrotaan kokonaismatkalla.
Kellon viisarit
Kellotaulun keskipiste on ruudukon kohdassa (0, 0). Tuntiviisarin pituus on 3 ja minuuttiviisarin pituus on 4. Mihin ruudukon pisteisiin viisarit osoittavat, kun kello on 16:52?
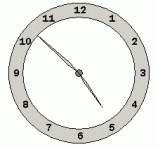
Kello 0:00 tuntiviisarin kulma on 90°. Viisari liikkuu 12 tunnissa 360° eli tunnissa 30° eli minuutissa 0,5°. Kello 16:52 minuutteja on kulunut 16 * 60 + 52 = 1012, eli tuntiviisarin kulma on 90° - 0,5° * 1012 = -416°. Tuntiviisari osoittaa pisteeseen (cos(-416°) * 3, sin(-416°) * 3) eli pisteeseen (1,68; -2,49).
Kello 0:00 minuuttiviisarin kulma on 90°. Viisari liikkuu tunnissa 360° eli minuutissa 6°. Kello 16:52 minuutteja on kulunut 1012, eli minuuttiviisarin kulma on 90° - 6° * 1012 = -5982°. Minuuttiviisari osoittaa pisteeseen (cos(-5982°) * 4, sin(-5982°) * 4) eli pisteeseen (-2,97; 2,68).
Lopuksi
Ohjelmointikielten trigonometriset funktiot käyttävät yleensä radiaaneja, minkä vuoksi radiaani on luonteva kulman ilmoitustapa ohjelmoinnissa. Jos erityistä syytä asteiksi muuttamiseen ei ole, kulmia kannattaa käsitellä läpi ohjelman radiaaneina.
Tässä oppaassa "ruudukko" on viitannut tavanomaiseen koordinaatistoon, jossa koordinaatit kasvavat oikealle ja ylös. Tietokoneen näytöllä koordinaatit kasvavat kuitenkin yleensä oikealle ja alas. Tämän takia kulman kiertosuunta trigonometrisissa funktioissa onkin myötäpäivään.
Voit lähettää tästä oppaasta palautetta sähköpostilla. Mistä matematiikan alueesta haluaisit seuraavan oppaan kertovan?
Antti Laaksonen, 5.1.2007
Kommentit
Jälleen hyvä opas! Vaikka suuren osan tuosta tiesin jo aiemmin, sain paljon hyvää nippelitietoa. Ja noita kellotaulun viisareiden kulmia en ole aiemmin miettinyt.
Jäi vain ihmetyttämään asteissa se, että mitä eroa on 0-asteella ja 360-asteella? Nythän asteita on yhteensä 361, eikä suinkaan 360. Eli ihmettelen mikä on ylimääräisen asteen tehtävä.
Lisäksi oppaassa lihavoitu fontti hämää yhdessä kohdassa:
"Kosinilause on laajennettu Pythagoraan lause, joka pätee kaikilla kolmioilla.
a2 = b2 + c2 - 2 * b * c * cos(α)"
Tuo kaava näyttää sivulla vähän siltä kuin kertomerkit (*) olisivat potenssimerkkejä (^). Asian oikea laita tulee tietysti esiin kun lukee opasta eteenpäin. :)
tkarkkainen [05.01.2007 23:23:24]
herkko kirjoitti:
Jäi vain ihmetyttämään asteissa se, että mitä eroa on 0-asteella ja 360-asteella? Nythän asteita on yhteensä 361, eikä suinkaan 360. Eli ihmettelen mikä on ylimääräisen asteen tehtävä.
Jos asteita käytetään kertomaan, mihin suuntaan jokin kappale osoittaa, 360 astetta on juuri tasan sama asia kuin nolla astetta.
Jos taas lasketaan vaikkapa sitä, kuinka pitkän matkan napakelkka kulkee pyörähtäessään x astetta, on erolla merkitystä. Jos x = 180, kelkka pyörähtää puolikkaan kierroksen. Jos x = 720, kelkka pyörähtää tasan kaksi kierrosta, ja kuljettu matka on nelinkertainen.
Ero nollan ja 360 asteen välillä riippuu siis tapauksesta. Trigonometristen käänteisfunktioiden kohdalla (joita tässä ei taidettu käsitellä) kannattaa huomata, että ne eivät anna arvoja kuin välillä -90...90 astetta (arcsin) ja 0...180 astetta (arccos).
Wihii, tämmöstä oon aina toivonut!
Jihuu, sarja jatkuu!
Ihan OK. Lisätietona sinilauseeseen vielä, että sinilauseessa suhde a/sin alfa on myös yhtä kuin 2R, missä R on kolmion ympäri piirretyn ympyrän säde. Ja eikös trigonometristen funktioiden käyttö ohjelmoinnissa ole hitaampaa kuin ottamalla riittävän tarkka polynomiapproksimaatio funktiosta? Tarkkuutta toki menetetään, mutta virhettäkin voi helposti arvioida.
Miksi muuten sinilausetta selittävässä kolmiossa kulmat ovat alfa, beeta ja khii eikä esim. alfa, beeta ja gamma? Itse kaavassa ei puhuta khiistä mitään.
Antti Laaksonen [08.01.2007 20:15:26]
Jaska kirjoitti:
Miksi muuten sinilausetta selittävässä kolmiossa kulmat ovat alfa, beeta ja khii - -
Varsin hyvä huomautus! Olin laittanut kuvaan väärän merkin.
Oppaan kirjoittaja, herra Laaksonen kirjoitti:
Missä kohdassa avaruusalus on sekunnin ja viiden sekunnin kuluttua?
Heh. Elikkä 1d and 5d = 001b and 101b = 1b = 1d :D
Mahtavaa, vaikken aivan tajunnutkaan.
Sini- ja kosinilauseet voisi laittaa omien otsikoidensa alle, niin näkyisivät sisällysluettelossa selvemmin.
Kerrassaan loistava opas, näillä tiedoilla selviääkin pitkälle.
Opas kirjoitti:
Esimerkki: Laske ympyrän kehäpisteen sijainti, kun kulma on 25°.
Vastaus: x = cos(20°) ≈ 0,94. y = sin(20°) ≈ 0,34. Kehälle päästään siis liikkumalla 0,94 oikealle ja 0,34 ylös.
Eikös vastaus ole: x = cos(25°) ja y = sin(25°) eikä 20:llä?
Antti Laaksonen [20.06.2007 22:02:29]
Olet oikeassa, nyt korjasin virheen.
Ny alakaa jotenki tajuta nuita.
"Ohjelmointikielten trigonometriset funktiot käyttävät yleensä radiaaneja, minkä vuoksi radiaani on luonteva kulman ilmoitustapa ohjelmoinnissa."
No astehan nyt on niin luonnoton viritys että huh huh..
Hyvä opas, tällä pääsee ihan kivaan alkuun!
Nyt vasta huomasin, että sini, kosini ja tangentti opetettiin meille kasilla mutta ope ei puhunut niistä noilla nimillä :O
Opas kirjoitti:
Esimerkki: Suorakulmaisen kolmion toisen kateetin pituus on 12 ja hypotenuusan pituus on 13. Mikä on toisen kateetin pituus?
Vastaus: a = 12 ja c = 13. 12^2 + b^2 = 13^2. b^2 = 169 - 144 = 25. b = v25 = 5. Siis toisen kateetin pituus on 5.
miten b^2 arvo on laskettu ? jos a ja c tunnetaan, ja b on tuntematon, ei voida tietää mitä 12^2 + b^2 on? Selittäisikö joku tämän minulle.. :)
Edit: Ahaa, 144 ja 169 ovat a^2 ja c^2. Esimerkkiin olisi voinut kuitenkin selvyyden vuoksi laittaa vaikka:
b^2 = c^2 - a^2 = 169 - 144 = 25
Edit2:
Freeze kirjoitti:
...ei voida tietää mitä 12^2 + b^2 on?
..niin voidaan kuitenkin olettaa, jos c arvon väitetään olevan 13..
Kirjoita kommentti
Huomio! Kommentoi tässä ainoastaan tämän oppaan hyviä ja huonoja puolia. Älä kirjoita muita kysymyksiä tähän. Jos koodisi ei toimi tai tarvitset muuten vain apua ohjelmoinnissa, lähetä viesti keskusteluun.