Oppaat: Ohjelmoijan matematiikka: Osa 3 - Vektorit
- Osa 1 - Jakojäännös
- Osa 2 - Pituus ja kulma
- Osa 3 - Vektorit
- Osa 4 - Tiedosta dataan
Kirjoittaja: Heikki (2007).
Tässä Ohjelmoijan matematiikka -opassarjan kolmannessa osassa käsitellään vektoreita. Vektorit ovat käytännössä välttämättömiä, kun ohjelmoidaan kaksi- tai kolmiulotteista grafiikkaa. Monet asiat ovat yksinkertaisesti lähes mahdottomia tehdä ilman vektoreita, esimerkkinä vaikkapa kimpoaminen kolmiulotteisessa avaruudessa.
Koska vektorit ovat monille täysin tuntematon käsite, käydään aluksi läpi vektoreiden perusasioita melko teoreettisesti. Lopussa tutustumme joihinkin tärkeimpiin perussovelluksiin, joita grafiikkaohjelmoinnissa tarvitaan.
Matematiikkaa ei voi oppia pelkästään lukemalla teoriaa, vaan harjoitustehtävien tekeminen on välttämätöntä. Tästä syystä oppaassa on yksinkertaisten laskuesimerkkien lisäksi myös harjoitustehtäviä pohdittavaksi. Alkupään tehtävät ovat helppoja, mutta lopuksi joudut jo vähän soveltamaan oppimaasi. Kaikkiin harjoitustehtäviin löytyy täydelliset ratkaisut.
Mikä on vektori?
Vektori (lat. vector, kantaja, vetäjä) on matemaattinen malli asialle, jolla on suunta ja suuruus. Esimerkiksi tuulen nopeus on vektori, sillä yleensä nopeuden lisäksi ilmaistaan myös, mihin suuntaan tuuli puhaltaa. Nopeuden lisäksi vektorisuureita ovat myös mm. kiihtyvyys ja voima.
Vektoria voidaan kuvata nuolella, jonka suunta on vektorin suunta ja pituus kuvaa vektorin pituutta. Oheiseen kuvaan on merkitty vektoreita eri tavoilla:
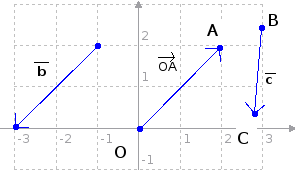
Yleinen tapa vektorien merkinnässä on pieni kirjain jonka päällä on viiva. Toinen yleinen tapa on merkitä vektori sen päätepisteiden mukaan, esimerkiksi kuvassa pisteestä O lähtevä ja pisteeseen A päättyvä vektori on siis vektori OA (yleensä pisteitä käytettäessä merkitään pisteiden yläpuolelle nuoli kuvaamaan vektorin suuntaa, mutta tässä se ei ole teknisistä syistä mahdollista). Kolmas, tässä oppaassa käytössä oleva, tapa on merkitä vektori lihavoidulla kirjaimella, esimerkiksi kuvassa c=BC.
Vektoria, joka lähtee origosta eli pisteestä (0,0), kutsutaan paikkavektoriksi, esimerkiksi kuvassa vektori OA on pisteen A paikkavektori.
Yleisesti kun pisteestä P1(x1,y1) muodostetaan vektori pisteeseen P2(x2,y2), se muodostetaan seuraavasti:
P1P2 = (x2-x1)i + (y2-y1)j
Huomaa, että päätepisteen koordinaatista vähennetään lähtöpisteen koordinaatti eikä päinvastoin! i ja j ovat kantavektorit, joita käsittelemme kappaleessa "Vektorien esittäminen koordinaatistossa".
Vaikka oheisessa kuvassa vektorit ovat kaksiulotteisessa koordinaatistossa, vektorin ei tarvitse sijaita koordinaatistossa ja sillä voi olla vaikka kuinka monta ulottuvuutta. Tässä oppaassa käsitellään kuitenkin (peli)ohjelmoinnin kannalta tärkeimpiä kaksi- ja kolmiulotteisia vektoreita koordinaatistossa. Lähes kaikki tässä oppaassa käsiteltävät asiat toimivat kuitenkin myös useampiulotteisille vektoreille. Jos vaikka pelihahmosi liikkuu 15-ulotteisessa avaruudessa, voit helposti käsitellä tilannetta vektoreilla. Kotitehtäväksi jää suunnitella, miltä 15-ulotteinen pelihahmo näyttää.
Merkintöjä
Vektoreille on määritelty seuraavia merkintöjä, joita käytetään myöhemmin tässä oppaassa:
- |a| tarkoittaa vektorin a pituutta.
- a||b tarkoittaa, että vektorit a ja b ovat yhdensuuntaiset (samansuuntaiset tai vastakkaissuuntaiset)
- a=b tarkoittaa, että a ja b ovat samat vektorit, eli niiden suunta ja suuruus ovat samat.
- -a tarkoittaa a:n vastavektoria, joka on yhtä pitkä kuin a mutta vastakkaissuuntainen.
Esimerkiksi kuvassa:
OA = -b
b||OA
Lisäksi on määritelty nollavektori, 0, jolla ei ole suuntaa ja jonka pituus on 0. Esimerkiksi vektori AA on nollavektori. Jos tuulta kuvataan vektorilla, niin tyyntä ilmaa kuvaisi nollavektori.
Merkintä a0 tarkoittaa a:n yksikkövektoria, joka on a:n kanssa samansuuntainen ja jonka pituus on 1. Yksikkövektori voidaan laskea seuraavalla kaavalla:
a0=a / |a|
Muodostettaessa yksikkövektori vektori siis jaetaan pituudellaan. Tätä kutsutaan myös vektorin normalisoinniksi.
Vektorien esittäminen koordinaatistossa
Kuten aiemmin jo todettiin, vektorien ulottuvuuksille ei ole olemassa ylärajaa. Ohjelmoinnissa käytetään kuitenkin lähes aina kaksi- ja kolmiulotteisia vektoreita, joten käsittelemme niitä.
Kun vektorit sijoitetaan koordinaatistoon, määritellään kantavektorit, jotka ovat koordinaatiston akseleiden (x, y ja z) suuntaisia yksikkövektoreita. X-akselin suuntaista kantavektoria merkitään vektorina i, y-akselin suuntainen on j ja z-akselin suuntainen k.
Seuraavassa kuvassa on esitetty vektori kaksiulotteisessa koordinaatistossa. Näkyviin on myös merkitty kantavektorit i ja j. Nyt yritämme ilmaista vektorin a kantavektorien avulla.
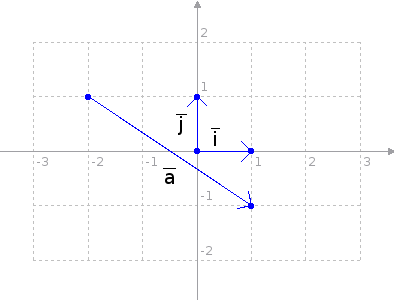
a kulkee kolme ruutua oikealle ja kaksi ruutua alas. Niinpä se kulkee kolme ruutua i:n suuntaan ja kaksi ruutua -j:n suuntaan. Voimme siis merkitä:
a = 3 * i + (-2) * j
Tai lyhyemmin
a = 3i - 2j
Koordinaatistossa vektorit esitetään siis kantavektorien monikertojen summana. Seuraavaksi käsittelemmekin tarkemmin vektorien yhteen- ja vähennyslaskun sekä kertomisen luvulla.
Vektorin komponenttiesitys
Koordinaatistossa oleva vektori voidaan siis esittää x- ja y-suuntaisten komponenttien avulla. Usein on tarve saada selville kyseisten komponenttien pituudet, kun tiedetään vektorin pituus ja kulma (esimerkiksi kun tiedetään pelaajahahmon suunta ja nopeus).
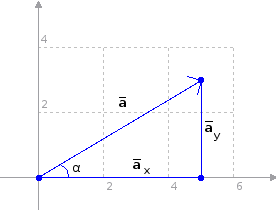
Jos merkitään vektorin ja positiivisen x-akselin välistä kulmaa kirjaimella α, saadaan suorakulmainen kolmio, josta voidaan helposti laskea trigonometrialla komponenttien pituudet. Y-akselin suuntainen komponentti on kolmiossa kulman α vastainen kateetti, jolloin voidaan käyttää siniä: kateetti = sin(kulma) * vektorin_pituus. Vastaavasti x-akselin suuntainen komponentti on kulman α viereinen kateetti, joten se saadaan samalla tavalla käyttämällä sinin sijaan kosinia. Oheisessa kuvassa siis:
ay = sin(α) * |a|
ax = cos(α) * |a|
Peruslaskutoimitukset
Vektorin yhteenlasku tarkoittaa sitä, että toinen vektori asetetaan alkamaan ensimmäisen päätepisteestä. Tällöin summavektori on vektori, jonka alkupiste on ensimmäisen vektorin alkupiste ja loppupiste toisen vektorin loppupiste. Vähennyslaskussa taas voidaan käyttää hyväksi seuraavaa tietoa:
a - b = a + (- b)
Siis vähennyslasku tarkoittaakin vektorin a ja vektorin b vastavektorin yhteenlaskua.
Asiaa havainnollistaa seuraava kuva:
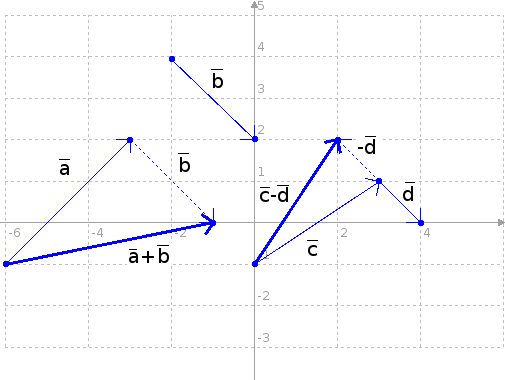
Kuten muistat, vektorilla ei ole paikkaa vaan ainoastaan suunta ja suuruus. Niinpä yhteenlaskussa a+b voidaan vektori b siirtää alkamaan vektorin a päätepisteestä, jolloin saadaan summavektori a+b.
Vähennyslaskussa c-d on taas on muodostettu vektorin d vastavektori -d ja asetettu se lähtemään vektorin c päätepisteestä, jolloin on saatu erotusvektori c-d.
Yhteenlaskujen suorittaminen piirtämällä ei kuitenkaan ole ohjelmoitaessa mahdollista eikä se ole muutenkaan kovin matemaattista. Koordinaatistossa olevien vektorien kesken voidaan yhteenlasku (ja samalla myös vähennyslasku) suorittaa laskemalla vektorien komponentit yhteen.
Esimerkki: Laske vektorien a = 2i - 2j ja b = i + 9j summa ja erotus.
Vastaus:
Summa:
a + b = 2i - 2j + i + 9j = (2 + 1)i + (-2 + 9)j = 3i + 7j.
Erotus:
a - b = 2i - 2j - (i + 9j) = 2i - 2j - i - 9j = (2 - 1)i + (-2 - 9)j = i -11j.
Vektorin kertominen skalaariluvulla (eli tavallisella reaaliluvulla) pitäisi jo näiden esimerkkien jälkeen olla selvää, olemmehan kertoneet kantavektoreita jo esimerkeissämme. Kun vektori kerrotaan luvulla, uusi vektori on kerrottavan vektorin kanssa yhdensuuntainen ja sen pituus on alkuperäisen vektorin pituus kerrottuna kertoimen itseisarvolla. Yksikkövektorien avulla ilmaistuna kertolasku lasketaan seuraavalla tavalla:
Esimerkki: a = 3i - k, laske -2/3 * a.
Vastaus: -2/3 * a = -2/3 * (3i - k) = (-2/3 * 3) i - (-2/3) k = -2i + 2/3k
Vektorin kertominen toisella vektorilla ei onnistu tällä tavalla. Tässä oppaassa käsitellään myöhemmin pistetulo ja ristitulo, jotka ovat kahden vektorin välisiä "kertolaskuja".
Edellä esitetyille laskutyypeille pätevät samat vaihdannaisuuslait kuin tavallisillekkin luvuille, esimerkiksi:
a+b = b + a = b - (-a)
4 * (a + b) = 4a + 4b
Vektorin pituus
Vektorin pituuden laskeminen onnistuu helposti Pythagoraan lauseella a^2 + b^2 = c^2, sillä kaksiulotteisessa koordinaatistossa vektorin kantavektoreita voidaan ajatella suorakulmaisen kolmion kateetteina ja itse vektoria sen hypotenuusana. Siis
a = i - 3j,
|a| = √12 + (-3)2 = √1 + 9 = √10 ≈ 3,16
Kolmiulotteisten vektorien tapauksessa vektorin pituus lasketaan samalla tavalla, neliöjuuren sisään vain otetaan lisäksi kolmannen kantavektorin kertoimen neliö:
b = 2i + 2j - 4k,
|b| = √22 + 22 + 42 = √4 + 4 + 16 = √24 = 2*√6 ≈ 4,9
Menetelmän perustelu (a, b ja d ovat vektorin komponentit eli kantavektori * luku, esimerkkimme tapauksessa a=2, b=2 ja d=4).
Harjoitustehtävä 1: Olkoon a = 6i - 2j + 3k. Määritä a0.
Pistetulo
Pistetulo on eräänlainen vektorien kertolasku, jonka tuloksena on tavallinen skalaariluku (tästä syystä pistetulosta käytetään joskus nimitystä skalaaritulo). Pistetulo määritellään seuraavalla tavalla:
a · b = |a| * |b| * cos(a, b)
Eli pistetulo on vektorien pituuksien tulo kertaa niiden välisen kulman kosini.
Pistetulo-operaattorina käytetään usein rivin keskellä olevaa pistettä ·. Pistetulo a·b luetaan "a piste b".
Koordinaatistossa oleville vektoreille pistetulon määrittäminen on helppoa, esimerkiksi kaksiulotteisessa koordinaatistossa pistetulo on i:n ja j:n kertoimien tulojen summa. Se, että näin on mahdollista tehdä, todistetaan oppaan lisämateriaalissa, johon on linkki oppaan lopussa.
Esimerkki: Olkoon a = 3i - 2j ja b = -i + 4j. Laske a · b.
Ratkaisu:: a · b = 3 * (-1) + (-2) * 4 = -3 - 8 = -11
Pistetulolle on voimassa lähes samanlaiset laskusäännöt kuin tavallisille kertolaskuille. Pistetulo on vaihdannainen, eli a · b = b · a, ja myös osoittelulaki on voimassa:
a · (b + c) = a · b + a · c
Lisäksi on olemassa lukutekijän siirtosääntö:
sa · b = a · (sb) = s ( a · b )
Vaikka äkkiseltään voi olla vaikea keksiä pistetulolle hyötykäyttöä, se on tuiki tarpeellinen monessa asiassa, kuten myöhemmin tässä oppaassa huomataan.
Harjoitustehtävä 2: Osoita, että yllä esitetyt laskusäännöt pätevät kaksiulotteisille vektoreille.
Vektorien välinen kulma
Pistetulo on avainasemassa, kun ratkaistaan vektorien välistä kulmaa. Aiemmin esitetystä pistetulon määritelmästä saadaan pyöritettyä muoto
cos(a, b) = ( a · b ) / ( |a| * |b| )
Eli vektorien välisen kulman kosini on vektorien pistetulo jaettuna niiden pituuksien tulolla.
Tästä seuraa myös eräs pistetulon ominaisuus: jos vektorien pistetulo on 0, vektorit ovat tällöin kohtisuorassa toisiaan vastaan (cos 90° = 0).
Harjoitustehtävä 3: Vektori a on muotoa a = 2i - 7j + xk ja b = i + 18j - k. Määritä x siten, että a on kohtisuorassa vektoria b vastaan.
Ristitulo
Ristitulo on kolmiulotteisen avaruuden vektoreille määritetty eräänlainen vektorien välinen kertolasku, jonka tuloksena on vektori, joka on kohtisuorassa molempia vektoreita vastaan ja jonka pituus on alkuperäisten vektorien määräämän suunnikkaan pinta-ala.
Ristitulo määritellään seuraavasti:
a × b = N*|a|*|b|*sin(a, b)
Missä N on vektoreita a ja b vastaan kohtisuora yksikkövektori.
Selkeytetäänpä vähän kuvalla:
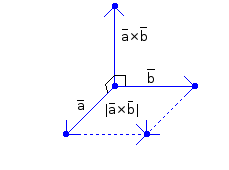
Kuvaan on merkitty vektorien a ja b välinen ristitulo a × b (luetaan "a risti b").
Ristitulon laskeminen ei ole yhtä helppoa kuin aiemmat vektorilaskut, kaava saattaa näyttää hieman monimutkaiselta:
Olkoon a = x1i + y1j + z1k ja b = x2i + y2j + z2k. Tällöin ristitulo on:
a × b = ( y1*z2 - z1*y2)i + (z1*x2 - x1*z2)j + (x1*y2 - y1*x2)k
Huomaa! Ristitulo ei ole vaihdannainen, eli axb ≠ b×a!
Tuossa muodossa kaava on vaikeasti muistettava, mutta toisaalta helposti ohjelmoitavissa. Kun ristitulo lasketaan paperilla, käytetään yleensä matriisimatematiikkaa apuna, jolloin kaava saadaan helposti muistettavaan muotoon. Ristitulon laskeminen matriisien avulla on esitelty oppaan lisämateriaalissa.
Ristitulon hyödyllisin piirre on se, että sen avulla saadaan helposti laskettua kahta vektoria vastaan kohtisuorassa oleva vektori. Tämä on tärkeää, kun myöhemmin puhumme normaalivektoreista ja tasoista kolmiulotteisessa avaruudessa. Toinen ristitulovektorin ominaisuus on se, että jos vektorit a ja b ovat suunnikkaan sivuvektorit, suunnikkaan pinta-ala on ristitulovektorin a×b pituus, eli A = |a×b|.
Kun katsot edellä olevaa kuvaa huomaat, että yhtä laillahan ristitulovektori, eli määritelmässä ollut vektori N, voisi osoittaa alaspäin (eli olisi vastakkaissuuntainen kuvaan merkittyä vektoria a×b vastaan). Tällöinkin vektori olisi kohtisuorassa vektoreita a ja b vastaan. Ristitulovektorin suunta voidaan kuitenkin päätellä oikean käden säännön avulla: jos oikean käden etusormi osoittaa vektorin a suuntaan ja keskisormi vektorin b suuntaan, peukalo osoittaa vektorin a×b suuntaan. Toisenlainen oikean käden sääntö kuuluu seuraavasti: jos oikean käden sormet peukaloa lukuun ottamatta osoittavat ensin vektorin a suuntaan ja niitä sitten taivutetaan kohti vektorin b suuntaa, peukalo osoittaa vektorin a×b suuntaan. Tästä voidaan päätellä ristitulolle seuraavanlainen "vaihdannaisuus":
a×b = -(b×a).
Ristitulovektorin suuntaa voidaan hyödyntää laskettaessa ristituloa kaksiulotteisen avaruuden vektoreille. "2D-ristitulohan" on periaatteessa vain skalaariluku, sillä kun katsotaan aiemmin esittelemääni ristitulon kaavaa huomataan, että z-suuntaisten komponenttien ollessa nollia, ovat ristitulovektorin sekä x- että y-suuntaiset komponentit nollia. Eli:
d=x1*y2 - y1*x2
Tärkeä sovellus "2D-ristitulolle" on seuraavanlainen tapahtuma: koordinaatistossa on pisteet, p, q ja r. Jos kuljetaan pisteestä p pisteeseen q ja siitä edelleen pisteeseen r, tehdäänkö pisteessä q käännös oikealle vai vasemmalle? Käännös tehdään oikealle, jos ristitulo
(r-p)×(q-p)
on positiivinen. Ristitulon ollessa nolla pisteet ovat samalla suoralla. Tällaisessa merkinnässä r-p tarkoittaa vektoria, joka lähtee pisteestä p ja päätyy pisteeseen r. Tätä ominaisuutta voidaan soveltaa esimerkiksi törmäystarkistuksessa, katso koodivinkki Törmäystarkistus 3D-avaruudessa: Jana ja kolmio.
Harjoitustehtävä 4: Osoita, että vektori n = -4i - 2j + 8k on kohtisuorassa vektoreita a = 3i - 2j + k ja b = -2i - k vastaan. Tee tehtävä käyttäen sekä ristituloa että pistetuloa.
Normaalivektori
Kolmiulotteisessa avaruudessa normaalivektori on kohtisuorassa kahta muuta vektoria (tai vaikka tasoa, josta lisää myöhemmin) vastaan. Tämän osaammekin jo laskea ristitulolla, joten tässä keskitymme vain normaalivektorin laskentaan kaksiulotteisessa avaruudessa.
Jos vektori on muotoa a = xi + yj, niin sitä vastaan kohtisuorassa ovat vektorit b = -yi + xj ja c = yi + -xj. Tämä voidaan helposti todeta laskemalla pistetulo (muistathan, että jos pistetulo on 0, vektorit ovat kohtisuorassa toisiaan vastaan):
a · b = x*(-y) + y*(x) = -xy + yx = 0
a · c = x*y + y*(-x) = xy - yx = 0
Itse asiassa b ja c ovat toistensa vastavektorit, eli b = -c.
Peiliheijastus
Nyt vektorimatematiikan perusteiden jälkeen olemme valmiita käsittelemään peliohjelmoinnin kannalta käytännöllisempiä asioita. Ensimmäinen niistä on peiliheijastus.
Peiliheijastus tapahtuu nimensä mukaisesti esimerkiksi silloin, kun valonsäde heijastuu peilistä. Muita peiliheijastuksia ovat muun muassa kimpoamiset. Vektorien avulla peiliheijastuksen laskeminen on helppoa ja nopeaa, emme tarvitse esimerkiksi lainkaan hitaita trigonometrisia funktioita.
Tarkastellaan esimerkkinä yksinkertaista tilannetta, jossa pallo kimpoaa vinosta seinästä kaksiulotteisessa maailmassa. Merkitään pallon nopeusvektoria v = 3i - j. Jos seinä kulkee pisteiden (1,0) ja (4,2) kautta, on se vektorin s = 3i + 2j suuntainen. Lasketaan tästä normaalivektori seinälle, sehän on edellisen kappaleen tietojen mukaisesti N = 2i - 3j. Jotta kohta käyttämämme kaava toimisi, on normaalivektori normalisoitava, eli siitä on tehtävä yksikkövektori (yleensä normaalivektorit kannattaa normalisoida heti aluksi laskennan helpottamiseksi). Normalisoitu normaalivektori on siis N = 1/√13 * (2i - 3j).
Nyt kun pallo heijastuu seinästä, sen uusi nopeusvektori saadaan laskettua kaavalla:
v2 = v - 2 * (v · N) * N
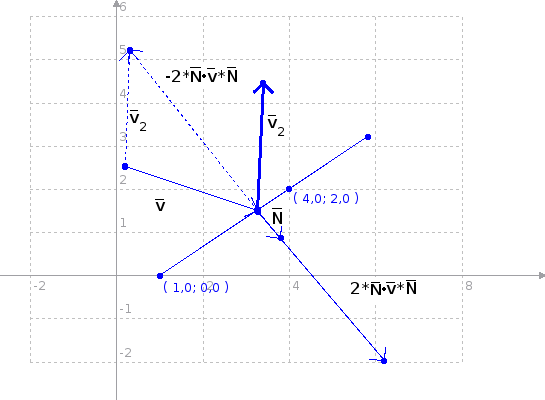
Kuvassa näkyy käsittelemämme tilanne. Lasketaanpa vielä heijastusvektori v2 vaihe vaiheelta.
Lasketaan ensin pistetulo v · N:
v · N = (3i - j) · 1/√13 (2i - 3j) = 1/√13 * (3*2 - 1*(-3)) = 9/√13 ≈ 2,5
Heijastusvektori on siis
v2 = v - 2*2,5*N = 3i - j - 5*(2/√13i - 3/√13j) ≈ 0,2i + 3,2j
Kuvaan vertaamalla nähdään, että tulos on luultavasti oikea.
Harjoitustehtävä 5: Laserkynällä ammutaan pisteestä (-12, -1, 1) kohti peiliä, jonka normaalivektori on n = 6i - 2j + 3k. Säde törmää peiliin pisteessä (2, 6, 15). Minkä vektorin suuntaisena säde jatkaa peilaantumisen jälkeen?
Taso vektoreiden avulla
Matematiikan taso on äärettömän suuri pinta, jonka määrittelyssä tarvitaan kolme tason pistettä, jotka eivät ole samalla suoralla, tai sitten yksi tason piste ja kaksi tason suuntaista, keskenään erisuuntaista vektoria.
Piste P on tasolla T jos ja vain jos on olemassa reaaliluvut t ja q siten, että:
OP = OA + t*a + q*b,
missä OP on pisteen P paikkavektori, A jokin tason piste ja a ja b tason T kaksi erisuuntaista vektoria. Tässä siis kuljetaan ensin origosta tasolla olevaan pisteeseen A, jonka jälkeen kuljetaan jokin matka tason suuntaisten vektorien a ja b suuntaisesti.
Edellisestä kaavasta voidaan johtaa kaava tason pisteelle:
OP · N = d,
missä N on tason normaali (voidaan laskea a:n ja b:n ristitulon avulla) ja d vakio. Kaava todistetaan oppaan lisämateriaalissa.
Esimerkki: Onko piste P(4,6,2) tasolla, jonka määräävät pisteet A(3,7,1), B(4,1,3) ja C(1,0,9)?
Ratkaisu:
Muodostetaan ensin kaksi tason erisuuntaista vektoria:
AB = i - 6j + 2k
AC = -2i - 7j + 8k
Tason normaalivektori on kohtisuorassa kaikkia tason vektoreita vastaan. Kuitenkin, jos vektori on kohtisuorassa kahta tason erisuuntaista vektoria vastaan, se on kohtisuorassa kaikkia tason vektoreita vastaan. Normaalivektori saadaan siis laskettua helposti ristitulolla:
N = AB × AC = -34i - 12j - 19k
Ratkaistaan tason yhtälöstä vakio d normaalivektorin ja pisteen A avulla:
d = N · (3i + 7j + k) = -205
Sama tulos saataisiin käyttäen mitä tahansa muuta tason pistettä, esimerkiksi pistettä B tai C.
Lopuksi katsotaan, onko kysytyn pisteen P ja tason normaalivektorin välinen pistetulo sama:
N · (4i + 6j + 2k) = -246
Eli piste P ei ole tasolla.
Harjoitustehtävä 6: Kuinka pitkä matka on kuljettava pisteestä P(0,1,0) tasolle, jonka määräävät pisteet A(5,7,5), B(4,9,1) ja C(5,9,1) kun kuljetaan vektorin a=2i + j + 3k suuntaisesti?
Harjoitustehtävä 7: Edellisen tehtävän tapauksessa kuljetaan lyhyintä reittiä pisteestä P tason pisteeseen, joka on lähinnä P:tä. Mikä tällöin on kuljettava matka (eli pisteen P etäisyys tasosta)?
OP-avaruusalus jatkaa matkaansa
Jatketaanpa opassarjan edellisessä osassa tarkastelemamme OP-avaruusaluksen liikettä. Sovitaan, että avaruusalus on koordinaatiston pisteessä (2,1) ja liikkuu suuntaan 40° (kulma positiivisesta x-akselista vastapäivään) nopeudella 5 (ruutua aikayksikössä). Aluksen komentaja havaitsee paikallaan olevan bugin koordinaateissa (7,3) ja ampuu nopeudella 8 (aluksen suhteen) liikkuvan ohjuksen sitä kohti tarkoituksenaan liiskata ilkeä bugi.
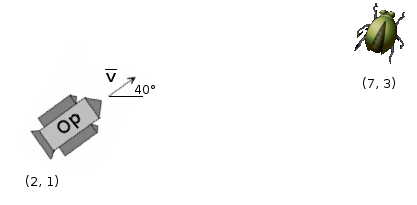
Tarkastellaan ohjuksen liikettä bugia kohti. Meidän on siis muodostettava ammuksen nopeusvektori.
Muodostetaan ensin aluksen nopeusvektori v:
v = 5 * cos 40° i + 5 * sin 40° j ≈ 3,83i + 3,21j
Ammuksen suunnan saamme arkustangentilla. Kuvitellaan, että vedämme janan aluksesta bugiin. Tämän janan kulmakerroin on y-koordinaattien erotus / x-koordinaattien erotus, ja kulma saadaan kulmakertoimesta arkustangentilla.
α = arctan (2/5) ≈ 21,8°
Kulman avulla saamme muodostettua ammuksen nopeusvektorin s aluksen suhteen:
s = 8 * cos 21,8° i + 8 * sin 21,8° j ≈ 7,43i + 2,97j
Kuitenkaan meitä ei kiinnosta ohjuksen nopeus aluksen suhteen, vaan tarvitsemme sen nopeusvektorin n koordinaatistossamme. Tämä vektori saadaan vektorisummana
n=v + s = (3,83 + 7,43)i + (3,21 + 2,97)j = 11,26i + 6,18j
Nyt voimmekin todeta helposti, että bugia ei saada liiskattua tällä ohjuksella: ohjuksen rata on periaatteessa puolisuora, jonka lähtöpiste on aluksen piste P = 2i + j ampumishetkellä ja suuntavektori n. Jokainen tämän puolisuoran pisteen paikkavektori X toteuttaa ehdon X = P + t*n, missä t on positiivinen reaaliluku. Jotta ohjus osuisi bugiin, bugin paikkavektorin tulisi toteuttaa tuo yhtälö:
7i + 3j = 2i + j + t*(11,26i + 6,18 j)
7i + 3j = (2 + t*11,26)i + (1 + t*6,18)j
Jolloin on oltava
2 + t*11,26 = 7
ja
1 + t*6,18 = 3
Ensimmäisestä yhtälöstä ratkeaa t=0,32, ja toisesta yhtälöstä t=0,44. Koska t:n arvot eivät ole samat, ohjus ei osu.
Lopuksi
Vektorilaskentaa varten ei ohjelmointikielissä yleensä ole valmiita työkaluja, mutta niiden ohjelmointi ei ole vaikeaa. Ja toisaalta vektorimatematiikka säilyy aina samana, joten kertaalleen tehtyä vektorilaskentakomponenttia voi käyttää aina uusissa projekteissa.
Jos haluat tutustua joihinkin oppaassa esiteltyihin asioihin hieman syvällisemmin, kannattaa vilkaista oppaan lisämateriaalia.
Voit lähettää kommentteja oppaaseen liittyen alla olevan kommentointialueen lisäksi sähköpostilla
Heikki Mäntysaari 28.2.2007
Viimeksi päivitetty 10.3.2007
Kommentit
Ihan hyvää ja selvää tekstiä.
Typo osiossa "Pistetulo": "siirtossäntö", tulisi olla "siirtosääntö".
Toka :(
Ja en ymmärtänyt oppaan sisuksia, pitänee lukea uudestaan :o
Ihan ok. Pari kommenttia:
Nollavektorilla ei ole suuntaa.
Nollavektorista ei voi muodostaa yksikkövektoria.
Nollavektori ei muodosta kulmaa x-akselin kanssa.
Wohoo, harvoin tulee vastaan matematiikasta oppaita joista saan jotain irti. Täs on kivasti selitetty hyödyllisiä jutskia joita voi käyttää peliohjelmoinnissa hyväksi :)
a kulkee 3 ruutua oikealle ja kaksi ruutua.
Lause kesken?
Hyvä opas pitää vain lueskella ajatuksella läpi :)
Vaikuttaa ihan kivalta, pitänee tutkia kotona paremmin.
Btw, sanat sekasin? "Vektoria voidaan kuvata kuvataan nuolella"
Kaikki (tai no ainakin tähän mennessä esiin tulleet) mokat korjattu.
Onkohan tuolla viitos tehtävän ratkaisussa virhe:
s = (2 − (−12))i + (6 − (−1))j + (15 − 1)k = −14i + 7j + 14k
miten (2-(-12)) :sta voi tulla -14
Jeps, virhehän siellä. Korjattu.
Hyvä opas, pitää vain ajatuksella lukea niin kyllä oppii. :)
edit: Noniin, nyt alkaa jo oppia. :D
Matikassa juuri aiheena vektorit, ihan opettavaista oli lukaista myös tämä läpi.
Vaikeeta on. Ei millään pysy mukana :/
6. tehtävän vastaus väärin: Laskin neliöjuurilaskun vastaukseksi n. 12,7 yksikköä. Ratkaisussa lukee n. 9,4 yksikköä.
Kirjoita kommentti
Huomio! Kommentoi tässä ainoastaan tämän oppaan hyviä ja huonoja puolia. Älä kirjoita muita kysymyksiä tähän. Jos koodisi ei toimi tai tarvitset muuten vain apua ohjelmoinnissa, lähetä viesti keskusteluun.